题目内容
13.在Rt△ABC中,∠C=90°,BC=15,CA=8,AB=17.分析 根据题意画出图形进而利用勾股定理得出AB的长.
解答  解:如图所示:∵∠C=90°,BC=15,CA=8,
解:如图所示:∵∠C=90°,BC=15,CA=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{1{5}^{2}+{8}^{2}}$=17.
故答案为:17.
点评 此题主要考查了勾股定理,正确应用勾股定理是解题关键.

练习册系列答案
相关题目
3.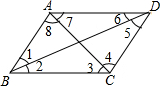 如图,由已知条件推出的结论,正确的是( )
如图,由已知条件推出的结论,正确的是( )
 如图,由已知条件推出的结论,正确的是( )
如图,由已知条件推出的结论,正确的是( )| A. | 由∠1=∠5,可以推出AD∥CB | B. | 由∠4=∠8,可以推出AD∥BC | ||
| C. | 由∠2=∠6,可以推出AD∥BC | D. | 由∠3=∠7,可以推出AB∥DC |
3.若x+x-1=a,则$\frac{{x}^{4}+1}{{x}^{2}}$等于(用含a的代数式表示)( )
| A. | a2+2 | B. | a2-2 | C. | a4+4 | D. | a4-4 |
 如图,是由6个正方体组成的图案,请分别画出它从左面看、右面看、上面看的平面图形.
如图,是由6个正方体组成的图案,请分别画出它从左面看、右面看、上面看的平面图形.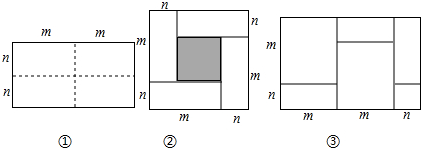
 如图,在Rt△ABC中,∠BAC=30°,AB=$\sqrt{3}$,将△ABC绕顶点C顺时针旋转至△A′B′C的位置,且A、CB′三点在同一条直线上,则点A经过的路线的长度是$\frac{4π}{3}$(结果保留π).
如图,在Rt△ABC中,∠BAC=30°,AB=$\sqrt{3}$,将△ABC绕顶点C顺时针旋转至△A′B′C的位置,且A、CB′三点在同一条直线上,则点A经过的路线的长度是$\frac{4π}{3}$(结果保留π).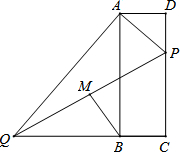 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.