题目内容
14.计算(1)(-x)3•(x5)2•x
(2)(3.14-π)0-2 -3+(-4)2÷($\frac{1}{2}$)-2
(3)50.2×49.8(简便运算)
(4)(2a+b)(b-2a)-(a-3b)2
(5)已知10m=2,10n=3,求103m+2n的值;
(6)已知9•32x•27x=317,求x的值.
分析 (1)先算乘方,再算乘法即可;
(2)先根据零整数指数幂、负整数指数幂以及乘方的意义分别化简,再进行加减运算即可;
(3)将式子变形为(50+0.2)(50-0.2),再利用平方差公式计算即可;
(4)先利用平方差公式与完全平方公式计算,再合并同类项即可;
(5)逆用同底数幂的乘法与幂的乘方的性质,原式=103m•102n=(10m)3•(10n)2,再代入计算即可;
(6)利用幂的乘方和同底数幂的乘法整理得出x的数值即可.
解答 解:(1)(-x)3•(x5)2•x
=-x3•x10•x
=-x14;
(2)(3.14-π)0-2 -3+(-4)2÷($\frac{1}{2}$)-2
=1-$\frac{1}{8}$+16÷4
=1-$\frac{1}{8}$+4
=4$\frac{7}{8}$;
(3)50.2×49.8
=(50+0.2)(50-0.2)
=2500-0.04
=2499.96;
(4)(2a+b)(b-2a)-(a-3b)2
=b2-4a2-a2+6ab-9b2
=-5a2+6ab-8b2;
(5)∵10m=2,10n=3,
∴103m+2n=103m•102n=(10m)3•(10n)2
=23•32
=8×9=72;
(6)∵9•32x•27x=32•32x•33x=32+2x+3x=317,
∴2+2x+3x=17,
∴x=3.
点评 此题考查了整式的混合运算,幂的运算性质,零整数指数幂、负整数指数幂以及乘方的意义,能够根据式子的特点,灵活选择解题方法是解决问题的关键.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
3.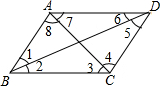 如图,由已知条件推出的结论,正确的是( )
如图,由已知条件推出的结论,正确的是( )
 如图,由已知条件推出的结论,正确的是( )
如图,由已知条件推出的结论,正确的是( )| A. | 由∠1=∠5,可以推出AD∥CB | B. | 由∠4=∠8,可以推出AD∥BC | ||
| C. | 由∠2=∠6,可以推出AD∥BC | D. | 由∠3=∠7,可以推出AB∥DC |
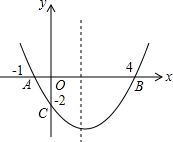 如图,在平面直角坐标系中,抛物线经过点A(-1,0),B(4,0),C(0,-2).
如图,在平面直角坐标系中,抛物线经过点A(-1,0),B(4,0),C(0,-2).