题目内容
12.已知下列一组数:1,$\frac{3}{4},\frac{5}{9},\frac{7}{16},\frac{9}{25}$,…;用代数式表示第n个数,则第n个数是$\frac{2n-1}{{n}^{2}}$.分析 观察已知5个分数可知,分子是连续的奇数,分母是序数的平方,据此可知第n个数.
解答 解:∵第1个数:1=$\frac{2×1-1}{{1}^{2}}$,
第2个数:$\frac{3}{4}$=$\frac{2×2-1}{{2}^{2}}$,
第3个数:$\frac{5}{9}$=$\frac{2×3-1}{{3}^{2}}$,
第4个数:$\frac{7}{16}$=$\frac{2×4-1}{{4}^{2}}$,
第5个数:$\frac{9}{25}$=$\frac{2×5-1}{{5}^{2}}$,
…
∴第n个数为:$\frac{2n-1}{{n}^{2}}$,
故答案为:$\frac{2n-1}{{n}^{2}}$.
点评 本题主要考查数字的变化规律,根据已知的数发现不变的部分和变化的部分,及变化部分是按何种规律变化是解此类问题的关键,通常需将变化部分与序数联系到一起.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
3.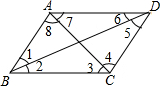 如图,由已知条件推出的结论,正确的是( )
如图,由已知条件推出的结论,正确的是( )
 如图,由已知条件推出的结论,正确的是( )
如图,由已知条件推出的结论,正确的是( )| A. | 由∠1=∠5,可以推出AD∥CB | B. | 由∠4=∠8,可以推出AD∥BC | ||
| C. | 由∠2=∠6,可以推出AD∥BC | D. | 由∠3=∠7,可以推出AB∥DC |
17.下列各式是二元一次方程的是( )
| A. | x+$\frac{1}{y}$=4 | B. | y=-2x | C. | $\frac{1}{2}$x+xy=2 | D. | x+y=a-1 |
 如图,是由6个正方体组成的图案,请分别画出它从左面看、右面看、上面看的平面图形.
如图,是由6个正方体组成的图案,请分别画出它从左面看、右面看、上面看的平面图形.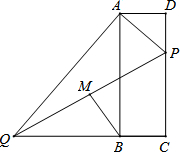 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.