题目内容
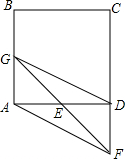 已知正方形ABCD,点E是边AD上一点(点E与点A、D不重合),点F在CD的延长线上,并保持DF=DE,连接FE并延长交AB于点G,假设
已知正方形ABCD,点E是边AD上一点(点E与点A、D不重合),点F在CD的延长线上,并保持DF=DE,连接FE并延长交AB于点G,假设| AD |
| DE |
考点:平行四边形的判定与性质,正方形的性质
专题:证明题
分析:根据正方形的性质,可得∠BAD=∠ADC,AB∥CD,根据全等三角形的判定与性质,可得AG=DF,根据平行四边形的判定与性质,可得答案.
解答:证明:∵四边形ABCD是正方形,
∴∠BAD=∠ADC,AB∥CD.
∵
=n=2,
∴E为AD的中点,
∴AE=DE,
在△AGE和△DFE中,
,
∴△AGE≌△DFE(ASA)
∴AG=DF,
又∵AG∥DF,
∴四边形AGDF是平行四边形,
∴AF∥GD.
∴∠BAD=∠ADC,AB∥CD.
∵
| AD |
| DE |
∴E为AD的中点,
∴AE=DE,
在△AGE和△DFE中,
|
∴△AGE≌△DFE(ASA)
∴AG=DF,
又∵AG∥DF,
∴四边形AGDF是平行四边形,
∴AF∥GD.
点评:本题考查了平行四边形的判定与性质,利用了正方形的性质,全等三角形的判定与性质,平行四边形的判定与性质.

练习册系列答案
相关题目
用两根长12cm的铁丝分别围成正方形和长与宽之比为2:1的长方形,则长方形和正方形的面积依次为( )
| A、9cm2和8cm2 |
| B、8cm2和9cm2 |
| C、32cm2和36cm2 |
| D、36cm2和32cm2 |
 已知在△FEC中,∠ACB=90°,AC=BC,∠ECF=135°,BE=x,BF=y.
已知在△FEC中,∠ACB=90°,AC=BC,∠ECF=135°,BE=x,BF=y.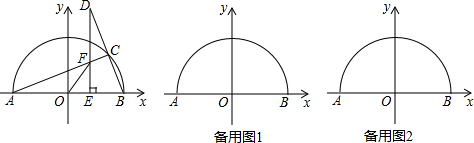
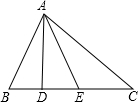 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=46°
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=46°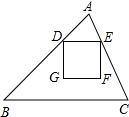 如图,在锐角△ABC中,BC=12,△ABC的面积为48,D、E分别是边AB、AC上的两个动点(D不与A、B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.
如图,在锐角△ABC中,BC=12,△ABC的面积为48,D、E分别是边AB、AC上的两个动点(D不与A、B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.