题目内容
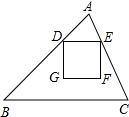 如图,在锐角△ABC中,BC=12,△ABC的面积为48,D、E分别是边AB、AC上的两个动点(D不与A、B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.
如图,在锐角△ABC中,BC=12,△ABC的面积为48,D、E分别是边AB、AC上的两个动点(D不与A、B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.(1)当正方形DEFG的边GF在BC上时,求正方形DEFG的边长;
(2)设DE=x,△ABC与正方形DEFG重叠部分的面积为y,试求y关于x的函数关系式,写出x的取值范围,并求出y的最大值.
(3)若tanB=4,连接FC,将△EFC沿直线EF翻折,点C的对称点为P点,求点P落在正方形DEFG内部时的x的取值范围.
考点:相似形综合题
专题:
分析:(1)如图1,过点A作BC边上的高AM,交DE于N,垂足为M.利用面积法求得AM=8;由相似三角形△ADE∽△ABC的对应边成比例、图中的相关线段间的和差关系得到
=
,易求DE=4.8;
(2)分两种情况:①当正方形DEFG在△ABC的内部时,②当正方形DEFG的一部分在△ABC的外部时,依据平行线以及正方形的性质,可得二次函数,再根据二次函数的性质,解可得重合部分的面积,比较可得面积的最大值;
(3)分类讨论:①当正方形DEFG的GF边在BC上时,可求得GF=4.8,BG=1.2,FC=6,显然点P不在正方形DEFG内部.
②随着边长的增大,正方形与BC相交,正方形与△ABC重叠部分为一个矩形.设DG与BC交于Q,EF与BC交于T,ET=y,由相似三角形△CTE∽△CMA、△ADE∽△ABC的对应边成比例得到:y=
,由图形知CT<QT,即
y<x,然后结合图形和该不等式来求x的取值范围.
| DE |
| 12 |
| 8-DE |
| 8 |
(2)分两种情况:①当正方形DEFG在△ABC的内部时,②当正方形DEFG的一部分在△ABC的外部时,依据平行线以及正方形的性质,可得二次函数,再根据二次函数的性质,解可得重合部分的面积,比较可得面积的最大值;
(3)分类讨论:①当正方形DEFG的GF边在BC上时,可求得GF=4.8,BG=1.2,FC=6,显然点P不在正方形DEFG内部.
②随着边长的增大,正方形与BC相交,正方形与△ABC重叠部分为一个矩形.设DG与BC交于Q,EF与BC交于T,ET=y,由相似三角形△CTE∽△CMA、△ADE∽△ABC的对应边成比例得到:y=
| 24-2x |
| 3 |
| 5 |
| 4 |
解答: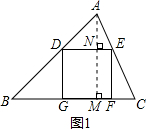 解:(1)当正方形DEFG的边GF在BC上时,如图1,过点A作BC边上的高AM,交DE于N,垂足为M.
解:(1)当正方形DEFG的边GF在BC上时,如图1,过点A作BC边上的高AM,交DE于N,垂足为M.
∵S△ABC=48,BC=12,
∴AM=8
∵DE∥BC,△ADE∽△ABC
∴
=
而AN=AM-MN=AM-DE
∴
=
解之得 DE=4.8
∴当正方形DEFG的边GF在BC上时,正方形DEFG的边长为4.8.
(2)分两种情况:
①如图2,当正方形DEFG在△ABC的内部时,△ABC与正方形DEFG重叠部分的面积为正方形DEFG的面积.
∵DE=x,
∴y=x2,此时x的范围是0<x≤4.8.
②如图3,当正方形DEFG的一部分在△ABC的外部时,设DG与BC交于点Q,EF与BC交于点T,△ABC的高AM交DE于N,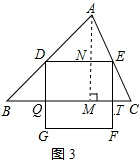
∵DE=x,DE∥BC,
∴△ADE∽△ABC
即
=
而AN=AM-MN=AM-ET
∴
=
解得 ET=8-
x
所以y=x(8-
x)
即y=-
x2+8x
由题意,x>4.8,x<12,
∴4.8<x<12
∴△ABC与正方形DEFG重叠部分的面积为y=
当0<x≤4.8时,△ABC与正方形DEFG重叠部分的面积的最大值为4.82=23.04
当4.8<x<12时,∴y=-
x2+8x,
∴当x=-
=6时,△ABC与正方形DEFG重叠部分的面积的最大值为
=24
∵24>23.04,
∴△ABC与正方形DEFG重叠部分的面积的最大值为24.
(3)AM⊥BC于M,可得AM=8
∵tanB=4,
∴BM=2,
∴CM=10
①当正方形DEFG的GF边在BC上时,可求得GF=4.8,BG=1.2,FC=6,显然点P不在正方形DEFG内部.
②随着边长的增大,正方形与BC相交,正方形与△ABC重叠部分为一个矩形.
设DG与BC交于Q,EF与BC交于T,ET=y,
∵△CTE∽△CMA
∴
=
,
∴CT=
y
∵△ADE∽△ABC
∴
=
,
∴y=
,
∵点P在正方形内,
∴CT<QT,即
y<x
∴
•
<x
∴x>
,
又x<12
∴点P落在正方形DEFG内部时的x的取值范围是
<x<12.
 解:(1)当正方形DEFG的边GF在BC上时,如图1,过点A作BC边上的高AM,交DE于N,垂足为M.
解:(1)当正方形DEFG的边GF在BC上时,如图1,过点A作BC边上的高AM,交DE于N,垂足为M.∵S△ABC=48,BC=12,
∴AM=8
∵DE∥BC,△ADE∽△ABC
∴
| DE |
| BC |
| AN |
| AM |
而AN=AM-MN=AM-DE
∴
| DE |
| 12 |
| 8-DE |
| 8 |
解之得 DE=4.8

∴当正方形DEFG的边GF在BC上时,正方形DEFG的边长为4.8.
(2)分两种情况:
①如图2,当正方形DEFG在△ABC的内部时,△ABC与正方形DEFG重叠部分的面积为正方形DEFG的面积.
∵DE=x,
∴y=x2,此时x的范围是0<x≤4.8.
②如图3,当正方形DEFG的一部分在△ABC的外部时,设DG与BC交于点Q,EF与BC交于点T,△ABC的高AM交DE于N,

∵DE=x,DE∥BC,
∴△ADE∽△ABC
即
| DE |
| BC |
| AN |
| AM |
而AN=AM-MN=AM-ET
∴
| x |
| 12 |
| 8-ET |
| 8 |
解得 ET=8-
| 2 |
| 3 |
所以y=x(8-
| 2 |
| 3 |
即y=-
| 2 |
| 3 |
由题意,x>4.8,x<12,
∴4.8<x<12
∴△ABC与正方形DEFG重叠部分的面积为y=
|
当0<x≤4.8时,△ABC与正方形DEFG重叠部分的面积的最大值为4.82=23.04
当4.8<x<12时,∴y=-
| 2 |
| 3 |
∴当x=-
| 8 | ||
2×(-
|
4×(-
| ||
4×(-
|
∵24>23.04,
∴△ABC与正方形DEFG重叠部分的面积的最大值为24.
(3)AM⊥BC于M,可得AM=8
∵tanB=4,

∴BM=2,
∴CM=10
①当正方形DEFG的GF边在BC上时,可求得GF=4.8,BG=1.2,FC=6,显然点P不在正方形DEFG内部.
②随着边长的增大,正方形与BC相交,正方形与△ABC重叠部分为一个矩形.
设DG与BC交于Q,EF与BC交于T,ET=y,
∵△CTE∽△CMA
∴
| y |
| 8 |
| CT |
| 10 |
∴CT=
| 5 |
| 4 |
∵△ADE∽△ABC
∴
| 8-y |
| 8 |
| x |
| 12 |
∴y=
| 24-2x |
| 3 |
∵点P在正方形内,
∴CT<QT,即
| 5 |
| 4 |
∴
| 5 |
| 4 |
| 24-2x |
| 3 |
∴x>
| 60 |
| 11 |
又x<12
∴点P落在正方形DEFG内部时的x的取值范围是
| 60 |
| 11 |
点评:本题主要考查了二次函数,平行线以及正方形的性质等知识点,要根据题意,得到二次函数关系,再根据二次函数的性质,即可得答案.

练习册系列答案
相关题目
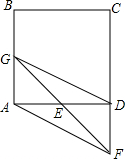 已知正方形ABCD,点E是边AD上一点(点E与点A、D不重合),点F在CD的延长线上,并保持DF=DE,连接FE并延长交AB于点G,假设
已知正方形ABCD,点E是边AD上一点(点E与点A、D不重合),点F在CD的延长线上,并保持DF=DE,连接FE并延长交AB于点G,假设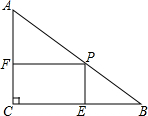 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,点P是AB边上的一个动点,过点P作PE⊥BC于点E,PF⊥AC于点F,当PB=
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,点P是AB边上的一个动点,过点P作PE⊥BC于点E,PF⊥AC于点F,当PB= 在Rt△ABC中,∠ABC=90°,AB=12,CB=8,中线AD、CF交于O,则OC=
在Rt△ABC中,∠ABC=90°,AB=12,CB=8,中线AD、CF交于O,则OC=