题目内容
 已知在△FEC中,∠ACB=90°,AC=BC,∠ECF=135°,BE=x,BF=y.
已知在△FEC中,∠ACB=90°,AC=BC,∠ECF=135°,BE=x,BF=y.(1)求证:∠ECA=∠F;
(2)若AE=2,求y与x的函数关系式.
考点:相似三角形的判定与性质,等腰直角三角形
专题:
分析:(1)利用等腰直角三角形的判定与性质得出∠CAE=180°-45°=135°,进而求出△ECA∽△CFB,即可得出答案;
(2)利用△ECA∽△CFB,则
=
,进而求出BE=x=AE+AB=2+2
,即可得出答案.
(2)利用△ECA∽△CFB,则
| AE |
| BC |
| AC |
| BF |
| y |
解答:(1)证明:∵∠ACB=90°,AC=BC,
∴△ABC为等腰直角三角形,
∴∠CAB=∠CBA=45°,
∴∠CAE=180°-45°=135°,
同理∠CBF=135°,
∴∠CAE=∠CBF,
∵∠ECF=135°,∠ACB=90°,
∴∠ECA+∠BCF=45°,
∵∠ECA+∠E=∠CAB=45°,
∴∠E=∠BCF,
∵∠CAE=∠CBF,
∴△ECA∽△CFB,
∴∠ECA=∠F;
(2)解:∵△ECA∽△CFB,
∴
=
,
即
=
,
∴BC•AC=BC2=2y,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AB2=2BC2=4y,
∴AB=2
,
∴BE=x=AE+AB=2+2
,
∴y=
(x-2)2.
∴△ABC为等腰直角三角形,
∴∠CAB=∠CBA=45°,
∴∠CAE=180°-45°=135°,
同理∠CBF=135°,
∴∠CAE=∠CBF,
∵∠ECF=135°,∠ACB=90°,
∴∠ECA+∠BCF=45°,
∵∠ECA+∠E=∠CAB=45°,
∴∠E=∠BCF,
∵∠CAE=∠CBF,
∴△ECA∽△CFB,
∴∠ECA=∠F;
(2)解:∵△ECA∽△CFB,
∴
| AE |
| BC |
| AC |
| BF |
即
| 2 |
| BC |
| AC |
| y |
∴BC•AC=BC2=2y,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AB2=2BC2=4y,
∴AB=2
| y |
∴BE=x=AE+AB=2+2
| y |
∴y=
| 1 |
| 4 |
点评:此题主要考查了相似三角形的判定与性质,得出△ECA∽△CFB是解题关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图,FE=BC,DE=AB,∠B=∠E=40°,∠F=70°,则∠A=( )
如图,FE=BC,DE=AB,∠B=∠E=40°,∠F=70°,则∠A=( )| A、40° | B、50° |
| C、60° | D、70° |
 如图,梯形ABCD中AD∥BC,∠B=90,P为DC上一点,PE⊥AB、PF⊥BC垂足分别为E、F,AD=1,AB=2,BC=5,BF=x,矩形EBFP面积为y,求y与x之间的函数关系式.
如图,梯形ABCD中AD∥BC,∠B=90,P为DC上一点,PE⊥AB、PF⊥BC垂足分别为E、F,AD=1,AB=2,BC=5,BF=x,矩形EBFP面积为y,求y与x之间的函数关系式.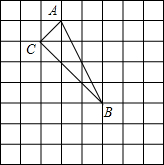 每个小正方形的边长为1.
每个小正方形的边长为1. 如图所示,过正方形ABCD的顶点A作对角线BD的平行线,在这条直线上取一点E,使BD=ED,且DE与AB交于点F,证明:BE=BF.
如图所示,过正方形ABCD的顶点A作对角线BD的平行线,在这条直线上取一点E,使BD=ED,且DE与AB交于点F,证明:BE=BF.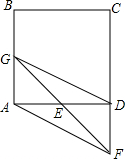 已知正方形ABCD,点E是边AD上一点(点E与点A、D不重合),点F在CD的延长线上,并保持DF=DE,连接FE并延长交AB于点G,假设
已知正方形ABCD,点E是边AD上一点(点E与点A、D不重合),点F在CD的延长线上,并保持DF=DE,连接FE并延长交AB于点G,假设