题目内容
已知四边形ABCD，∠B=∠ACD，AB=6，BC=4，AC=5，CD=7.5，求AD的长．
考点：相似三角形的判定与性质
专题：
分析：由条件可证明△ABC∽△DCA，再利用三角形相似的性质可得
=
，把数据代入即可求得AD．
| AC |
| AD |
| BC |
| AC |
解答：解：
∵AB=6，BC=4，AC=5，CD=7.5，
∴
=
=
，
且∠B=∠ACD，
∴△ABC∽△DCA，
∴
=
=
，
∴
=
，
∴AD=
．
∵AB=6，BC=4，AC=5，CD=7.5，
∴
| AB |
| CD |
| BC |
| AC |
| 4 |
| 5 |
且∠B=∠ACD，
∴△ABC∽△DCA，
∴
| AC |
| AD |
| BC |
| AC |
| 4 |
| 5 |
∴
| 5 |
| AD |
| 4 |
| 5 |
∴AD=
| 25 |
| 4 |
点评：本题主要考查三角形相似的判定和性质，解题的关键是由所给的线段长度得到线段的比相等．
练习册系列答案
春雨教育同步作文系列答案
相关题目
如图，梯形ABCD中AD∥BC，∠B=90，P为DC上一点，PE⊥AB、PF⊥BC垂足分别为E、F，AD=1，AB=2，BC=5，BF=x，矩形EBFP面积为y，求y与x之间的函数关系式．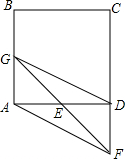
已知正方形ABCD，点E是边AD上一点（点E与点A、D不重合），点F在CD的延长线上，并保持DF=DE，连接FE并延长交AB于点G，假设
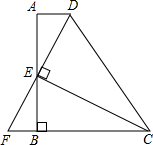已知，在梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC，E在AB上，DE⊥CE，DE延长线交BC延长线于F．