题目内容
2.上数学课时,老师给出了一个一元二次方程x2+ax+b=0,并告诉学生,从数字1、3、5、中随机抽取一个作为a,从数字2、6中随机抽取一个作为b,组成不同的方程共m个,其中有实数解的方程共n个,则$\frac{n}{m}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
分析 画树状图展示所有12种等可能的结果数,则m=12,根据判别式的意义可判断a=3,b=2;a=5,b=2;a=5,b=6时,方程有实数解,则n=3,然后计算$\frac{n}{m}$的值.
解答 解:画树状图:
共有12种等可能的结果数,则m=12,
其中a=3,b=2;a=5,b=2;a=5,b=6时,方程有实数解,则n=3,
所以$\frac{n}{m}$=$\frac{3}{6}$=$\frac{1}{2}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了根的判别式.

练习册系列答案
相关题目
10.Rt△ABC中,直角边AC=1,BC=2,则斜边AB的长度大约是( )
| A. | 在2和3之间 | B. | 在3和4之间 | C. | 在4和5之间 | D. | 在5和6之间 |
7.下列各组中代表的三条线段(a≠0)能组成三角形( )
| A. | 3a2,4a2,8a2 | B. | 5a2,6a2,11a2 | C. | 5a2,6a2,10a2 | D. | 4a2,4a2,8a2 |
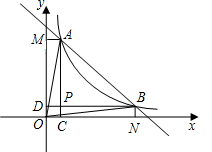 已知反比例函数y=$\frac{k}{x}$(k>0)的图象与直线y=-x+6相交于第一象限A、B的两点.如图所示,过A、B两点分别作x、y轴的垂线,线段AC、BD相交与P,给出以下结论:①OA=OB;②四边形OCPD是正方形;③若k=5.则△ABP的面积是8;④P点一定在直线y=x上,其中正确命题的个数是几个( )
已知反比例函数y=$\frac{k}{x}$(k>0)的图象与直线y=-x+6相交于第一象限A、B的两点.如图所示,过A、B两点分别作x、y轴的垂线,线段AC、BD相交与P,给出以下结论:①OA=OB;②四边形OCPD是正方形;③若k=5.则△ABP的面积是8;④P点一定在直线y=x上,其中正确命题的个数是几个( )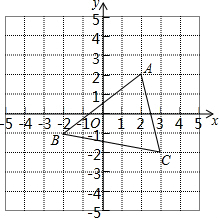 如图,将△ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度,得到△EFG.
如图,将△ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度,得到△EFG.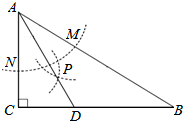 如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )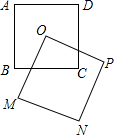 如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.
如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.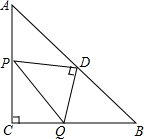 如图,等腰Rt△ABC中,∠C=90°,AC=BC,D是AB的中点,P是线段AC上的动点,连接PD,作DQ⊥PD交线段CB于Q,连接PQ,则点P从A向C方向运动过程中,△CPQ的面积变化是先逐渐增大,再逐渐减小.
如图,等腰Rt△ABC中,∠C=90°,AC=BC,D是AB的中点,P是线段AC上的动点,连接PD,作DQ⊥PD交线段CB于Q,连接PQ,则点P从A向C方向运动过程中,△CPQ的面积变化是先逐渐增大,再逐渐减小.