题目内容
19.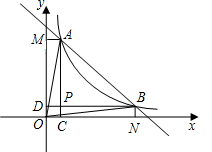 已知反比例函数y=$\frac{k}{x}$(k>0)的图象与直线y=-x+6相交于第一象限A、B的两点.如图所示,过A、B两点分别作x、y轴的垂线,线段AC、BD相交与P,给出以下结论:①OA=OB;②四边形OCPD是正方形;③若k=5.则△ABP的面积是8;④P点一定在直线y=x上,其中正确命题的个数是几个( )
已知反比例函数y=$\frac{k}{x}$(k>0)的图象与直线y=-x+6相交于第一象限A、B的两点.如图所示,过A、B两点分别作x、y轴的垂线,线段AC、BD相交与P,给出以下结论:①OA=OB;②四边形OCPD是正方形;③若k=5.则△ABP的面积是8;④P点一定在直线y=x上,其中正确命题的个数是几个( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 ①先求出直线y=-x+6与两坐标轴的交点坐标可得出△OEF是等腰直角三角形,故E、F两点关于直线y=x对称,再由反比例函数的图象关于直线y=x对称可知A、B两点关于直线y=x对称,故可得出y=x是线段AB的垂直平分线,由此即可得出结论;
②根据AM⊥y轴,BD⊥y轴,AC⊥x轴,BN⊥x轴可得出四边形ACOM与四边形BDON均是长方形,根据OA=OB可知AC=BD,故OC=OD,由此可得出结论;
③设A(x,$\frac{5}{x}$),则B($\frac{5}{x}$,x),P(x,x),再由点A在直线y=-x+6上,求出x的值即可得出A点坐标,再由三角形的面积公式求解即可;
④根据点A、B关于直线y=x对称可知,OM=ON,再由AM⊥y轴,AC⊥x轴,BD⊥y轴,BN⊥x轴可知,四边形AMOC与四边形BDON均是矩形,由②知AM=BN,故OC=OD,所以AP=PB,所以点P在线段AB的垂直平分线上,所以点P在直线y=x上.
解答  解:①∵令x=0,则y=6,令y=0,则x=6,
解:①∵令x=0,则y=6,令y=0,则x=6,
∴E(0,6),F(6,0),
∴E、F两点关于直线y=x对称,
∵反比例函数的图象关于直线y=x对称,
∴A、B两点关于直线y=x对称,
∴y=x是线段AB的垂直平分线,
∴OA=OB,故①正确;
②∵AM⊥y轴,BD⊥y轴,AC⊥x轴,BN⊥x轴,
∴四边形ACOM与四边形BDON均是长方形.
∵OA=OB,A、B两点关于直线y=x对称,
∴AC=BD,
∴OC=OD,
∴四边形OCPD是正方形,故②正确;
③设A(x,$\frac{5}{x}$),则B($\frac{5}{x}$,x),P(x,x),
∵点A在直线y=-x+6上,
∴-x+6=$\frac{5}{x}$,解得x1=1,x2=5,
∴A(1,5),B(5,1),
∴BP=AP=5-1=4,
∴S△ABP=$\frac{1}{2}$BP•AP=$\frac{1}{2}$×4×4=8,故③正确;
④∵点A、B关于直线y=x对称,
∴OM=ON,
∵AM⊥y轴,AC⊥x轴,BD⊥y轴,BN⊥x轴,
∴四边形AMOC与四边形BDON均是矩形,
∵由②知AM=BN,
∴OC=OD,
∴AP=PB,
∴点P在线段AB的垂直平分线上,
∴点P在直线y=x上,故④正确.
故选A.
点评 本题考查的是反比例函数综合题,熟知反比例函数及一次函数图象上点的坐标特点、正方形的判定与性质及关于直线y=x对称的点的坐标特点是解答此题的关键.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 4、6、5、10 | B. | 12、8、16、20 | C. | 1、2、3、4 | D. | 1、2、2、4 |
 某公园一喷水池喷水时水流的路线呈抛物线(如图).若喷水时水流的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+1.25,则水池在喷水过程中水流的最大高度为( )
某公园一喷水池喷水时水流的路线呈抛物线(如图).若喷水时水流的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+1.25,则水池在喷水过程中水流的最大高度为( )| A. | 1.25米 | B. | 2.25米 | C. | 2.5米 | D. | 3米 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
 如图,E是△ABC中AB边延长线上一点,∠EBC的平分线交AC延长线于点D,若∠A=40°,∠CBD=68°,求∠D的度数.
如图,E是△ABC中AB边延长线上一点,∠EBC的平分线交AC延长线于点D,若∠A=40°,∠CBD=68°,求∠D的度数.
 如图:AB∥CD,∠A=75°,∠C=35°,求∠E.
如图:AB∥CD,∠A=75°,∠C=35°,求∠E.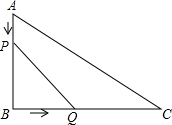 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.