题目内容
10．Rt△ABC中，直角边AC=1，BC=2，则斜边AB的长度大约是（ ）| A． | 在2和3之间 | B． | 在3和4之间 | C． | 在4和5之间 | D． | 在5和6之间 |
分析 由勾股定理求出AB=$\sqrt{5}$，由$\sqrt{4}＜\sqrt{5}＜\sqrt{9}$，得出2＜$\sqrt{5}$＜3即可．
解答 解：由勾股定理得：AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
∵$\sqrt{4}＜\sqrt{5}＜\sqrt{9}$，
∴2＜$\sqrt{5}$＜3，
故选：A．
点评 本题考查了勾股定理、估算无理数的大小；熟练掌握勾股定理，并能对无理数进行估算是解决问题的关键．
练习册系列答案
相关题目
5．
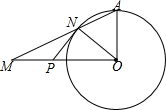如图，△AOM中，OA⊥OM，OA=2，以O为圆心，OA为半径作⊙O交AM于N，过点N作⊙O的切线交OM于P，若PM、PN为关于x的一元二次方程x2+（m-2）x+m+1=0的两根，求S△AOM．
如图，△AOM中，OA⊥OM，OA=2，以O为圆心，OA为半径作⊙O交AM于N，过点N作⊙O的切线交OM于P，若PM、PN为关于x的一元二次方程x2+（m-2）x+m+1=0的两根，求S△AOM． 
15．在△ABC中，∠C=80°，∠B=60°，那么∠A的度数是（ ）
| A． | 20° | B． | 40° | C． | 60° | D． | 70° |
2．上数学课时，老师给出了一个一元二次方程x2+ax+b=0，并告诉学生，从数字1、3、5、中随机抽取一个作为a，从数字2、6中随机抽取一个作为b，组成不同的方程共m个，其中有实数解的方程共n个，则$\frac{n}{m}$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
20．已知x+y=10，xy=24，则x2+y2的值为（ ）
| A． | 52 | B． | 148 | C． | 58 | D． | 76 |