题目内容
20.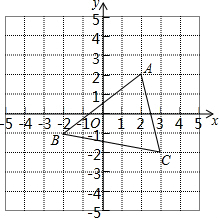 如图,将△ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度,得到△EFG.
如图,将△ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度,得到△EFG.①△EFG的三个顶点坐标是:E(4,1),F(0,-2),G (5,-3).
②在平面直角坐标系中画出△EFG,并求△EFG的面积.
分析 ①利用平移的性质得出对应点位置进而得出各点坐标;
②利用E,F,G的位置画出图形,进而利用△EFG所在矩形面积减去周围三角形面积进而得出答案.
解答  解:①E(4,1),F(0,-2),G(5,-3);
解:①E(4,1),F(0,-2),G(5,-3);
故答案为:(4,1),(0,-2),(5,-3);
②如图所示:△EFG即为所求,
△EFG的面积为:4×5-$\frac{1}{2}$×3×4-$\frac{1}{2}$×1×4-$\frac{1}{2}$×1×5=9.5.
点评 此题主要考查了平移变换以及三角形面积求法,根据题意得出各点位置是解题关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
5.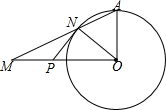 如图,△AOM中,OA⊥OM,OA=2,以O为圆心,OA为半径作⊙O交AM于N,过点N作⊙O的切线交OM于P,若PM、PN为关于x的一元二次方程x2+(m-2)x+m+1=0的两根,求S△AOM.
如图,△AOM中,OA⊥OM,OA=2,以O为圆心,OA为半径作⊙O交AM于N,过点N作⊙O的切线交OM于P,若PM、PN为关于x的一元二次方程x2+(m-2)x+m+1=0的两根,求S△AOM.
 如图,△AOM中,OA⊥OM,OA=2,以O为圆心,OA为半径作⊙O交AM于N,过点N作⊙O的切线交OM于P,若PM、PN为关于x的一元二次方程x2+(m-2)x+m+1=0的两根,求S△AOM.
如图,△AOM中,OA⊥OM,OA=2,以O为圆心,OA为半径作⊙O交AM于N,过点N作⊙O的切线交OM于P,若PM、PN为关于x的一元二次方程x2+(m-2)x+m+1=0的两根,求S△AOM.
2.上数学课时,老师给出了一个一元二次方程x2+ax+b=0,并告诉学生,从数字1、3、5、中随机抽取一个作为a,从数字2、6中随机抽取一个作为b,组成不同的方程共m个,其中有实数解的方程共n个,则$\frac{n}{m}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
3.在算式am+n÷□=am+2中,□内的代数式应是( )
| A. | am+n+2 | B. | an-2 | C. | am+n-2 | D. | an+2 |
 如图,E是△ABC中AB边延长线上一点,∠EBC的平分线交AC延长线于点D,若∠A=40°,∠CBD=68°,求∠D的度数.
如图,E是△ABC中AB边延长线上一点,∠EBC的平分线交AC延长线于点D,若∠A=40°,∠CBD=68°,求∠D的度数.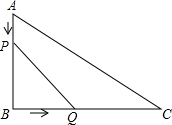 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.