题目内容
14.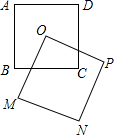 如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.
如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.
分析 OM交BC于E,OP交CD于F,连结OB、OC,如图,根据正方形的性质得∠OBC=90°,∠OBC=∠OCD=45°,∠MOP=90°,OB=OC,则利用等角的余角相等得∠BOE=∠COF,于是可根据“ASA”判断△BOE≌△COF,
所以S△BOE=S△COF,则S四边形OECF=S△OBC=$\frac{1}{4}$S正方形ABCD=25.
解答 解:OM交BC于E,OP交CD于F,连结OB、OC,如图,
∵四边形ABCD和四边形OMNP为正方形,
∴∠OBC=90°,∠OBC=∠OCD=45°,∠MOP=90°,OB=OC,
∵∠BOE+∠EOC=90°,∠FOC+∠EOC=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,
$\left\{\begin{array}{l}{∠OBE=∠OCF}\\{OB=OC}\\{∠BOE=∠COF}\end{array}\right.$,
∴△BOE≌△COF,
∴S△BOE=S△COF,
∴S四边形OECF=S△OBC=$\frac{1}{4}$S正方形ABCD=$\frac{1}{4}$×10×10=25,
即这两个正方形重叠部分的面积为25.
故答案为25.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.上数学课时,老师给出了一个一元二次方程x2+ax+b=0,并告诉学生,从数字1、3、5、中随机抽取一个作为a,从数字2、6中随机抽取一个作为b,组成不同的方程共m个,其中有实数解的方程共n个,则$\frac{n}{m}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
3.在算式am+n÷□=am+2中,□内的代数式应是( )
| A. | am+n+2 | B. | an-2 | C. | am+n-2 | D. | an+2 |
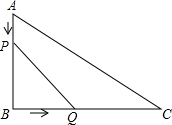 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.