题目内容
13.如图,在△ABC中,AB=AC,AD平分∠BAC,O是AC的中点,连接DO,过点C作CE∥DA,交DO的延长线于点E,连接AE.
(1)求证:四边形ADCE是矩形;
(2)若F是CE上的动点(点F不与C、E重合),连接AF、DF、BE,请直接写出图2中与四边形ABDF面积相等的所有的三角形和四边形(四边形ABDF除外)
分析 (1)根据全等三角形的判定求出△ADO≌△CEO,求出OD=OE,根据平行四边形的判定得出四边形ADCE是平行四边形,再根据矩形的判定得出即可;
(2)根据面积公式和等底等高的三角形的面积相等得出即可.
解答 (1)证明:∵CE∥DA,
∴∠OCE=∠OAD,
∵O为AC的中点,
∴OA=OC,
在△ADO和△CEO中
$\left\{\begin{array}{l}{∠OAD=∠OCE}\\{OA=OC}\\{∠DOA=∠EOC}\end{array}\right.$
∴△ADO≌△CEO(ASA),
∴OD=OE,
∵OA=OC,
∴四边形ADCE是平行四边形,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADC=90°,
∴平行四边形ADCE是矩形;
(2)解:图2中与四边形ABDF面积相等的所有的三角形和四边形有△ABC,△BCE,矩形ADCE,四边形ABDE,
理由是:∵△ACD和△AFD的面积相等(等底等高的三角形面积相等),
∴S△ADC=S△ADF,
∴S△ADC+S△ADB=S△ADF+S△ADB,
∴S四边形ABDF=S△ABC;
∵S△BCE=S△ABC,
∴S四边形ABDF=S△BCE;
∵S△ADB=S△ADC,S△ADF=S△AEC,
∴S四边形ABDF=S矩形ADCE;
∵S△ADF=S△ADE,
∴都加上△ADB的面积得:S四边形ABDF=S四边形ABDE.
点评 本题考查了矩形的判定,平行四边形的判定,全等三角形的性质和判定的应用,能正确根据定理进行推理是解此题的关键,注意:有一个角是直角的平行四边形是矩形.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
8.已知∠1和∠2的两边互相平行,已知∠1=40°,则∠2=( )
| A. | 40° | B. | 140° | C. | 40°和50° | D. | 40°或140° |
 如图,四边形ABCD中,AD∥BC,AF,DE分别平分∠BAD和∠ADC,AF与DE相交于点G,AF⊥DE.判断四边形ABCD的形状,并证明.
如图,四边形ABCD中,AD∥BC,AF,DE分别平分∠BAD和∠ADC,AF与DE相交于点G,AF⊥DE.判断四边形ABCD的形状,并证明. 如图,在Rt△ABC中,∠ACB=Rt∠,AC=3,BC=4,⊙O内切于△ABC,D,E,F为切点,直线CO交AB于点G.求DG的长.
如图,在Rt△ABC中,∠ACB=Rt∠,AC=3,BC=4,⊙O内切于△ABC,D,E,F为切点,直线CO交AB于点G.求DG的长.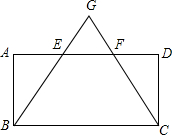 如图,在平行四边形ABCD中,E、F为AD上两点,AE=EF=FD,连接BE、CF并延长,交于点G,GB=GC.
如图,在平行四边形ABCD中,E、F为AD上两点,AE=EF=FD,连接BE、CF并延长,交于点G,GB=GC.