题目内容
10.已知AB是⊙O的弦,用直尺和圆规作以AB为边的圆内接等腰三角形,若这样的三角形恰好能作两个,则AB:OA=2:1或$\sqrt{3}$:1.分析 分类讨论:当以AB为底边作一个等边△ACB和等腰△AC′B时,如图1,作OH⊥AB于H,利用垂径定理得到AH=BH,再利用点O为等边△ACB的内心得到∠OAH=30°,则根据余弦的定义可求出$\frac{AH}{OA}$=$\frac{\sqrt{3}}{2}$,所以AB:OA=$\sqrt{3}$:1;当以AB为底边作两个等腰Rt△ACB和Rt△AC′B时,如图2,根据圆周角定理得到AB为直径,于是有AB:OA=2:1.
解答 解:当以AB为底边作一个等边△ACB和等腰△AC′B时,如图1,作OH⊥AB于H,则AH=BH,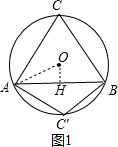
点O为等边△ACB的内心,∠OAH=30°,
在Rt△OAH中,∵cos∠OAH=$\frac{AH}{OA}$=cos30°=$\frac{\sqrt{3}}{2}$,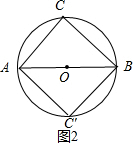
∴AB:OA=$\sqrt{3}$:1;
当以AB为底边作两个等腰Rt△ACB和Rt△AC′B时,如图2,
因为∠C=∠C′=90°,所以AB为直径,
所以AB:OA=2:1.
故答案为2:1或$\sqrt{3}$:1.
点评 本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆.三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.解决本题的关键是画出几何图形.

练习册系列答案
相关题目
15.甲、乙两名射击运动员在某场测试中各射击20次,甲、乙两人的测试成绩如下表,则测度成绩比较稳定的是( )
| 甲的成绩 | 乙的成绩 | ||||||||||
| 环数 | 6 | 7 | 8 | 9 | 10 | 环数 | 6 | 7 | 8 | 9 | 10 |
| 频数 | 3 | 5 | 4 | 5 | 3 | 频数 | 5 | 3 | 4 | 3 | 5 |
| A. | 甲 | B. | 乙 | ||
| C. | 甲、乙两人成绩稳定程度相同 | D. | 无法确定 |
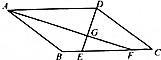 如图,四边形ABCD中,AD∥BC,AF,DE分别平分∠BAD和∠ADC,AF与DE相交于点G,AF⊥DE.判断四边形ABCD的形状,并证明.
如图,四边形ABCD中,AD∥BC,AF,DE分别平分∠BAD和∠ADC,AF与DE相交于点G,AF⊥DE.判断四边形ABCD的形状,并证明. 如图,在Rt△ABC中,∠ACB=Rt∠,AC=3,BC=4,⊙O内切于△ABC,D,E,F为切点,直线CO交AB于点G.求DG的长.
如图,在Rt△ABC中,∠ACB=Rt∠,AC=3,BC=4,⊙O内切于△ABC,D,E,F为切点,直线CO交AB于点G.求DG的长.