题目内容
若x、y为非负实数,且方程组
有解,则a的值为( )
|
| A、0 | B、-2 | C、2 | D、不定 |
考点:二元一次方程组的解
专题:
分析:先把a当作已知求出x、y的值,再根据方程组有非负实数解得到关于a的一元一次不等式组,求出a的取值范围,再找出符合条件的a的值即可.
解答:解:
,
解得:
,
∵x、y为非负实数,
∴x≥0且y≥0,
即:
,
解得:a≥-2且a≤-2,
∴a=-2.
故选:B.
|
解得:
|
∵x、y为非负实数,
∴x≥0且y≥0,
即:
|
解得:a≥-2且a≤-2,
∴a=-2.
故选:B.
点评:本题考查的是解二元一次方程组及解一元一次不等式组,解答此题的关键是先把a当作已知表示出x、y的值,再根据方程组有非负实数解得出关于a的不等式组,求出a的值即可.

练习册系列答案
相关题目
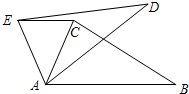 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A、30° | B、35° |
| C、40° | D、50° |
 如图,直线l是四边形ABCD的对称轴,若AB=CD,有下面的结论:①AB⊥BC;②AC⊥BD;③AB∥CD;④AO=OC.其中正确的结论有
如图,直线l是四边形ABCD的对称轴,若AB=CD,有下面的结论:①AB⊥BC;②AC⊥BD;③AB∥CD;④AO=OC.其中正确的结论有 如图,在△ABD中,∠A=∠B=30°,以AB边上一点O为圆心,过A,D两点作⊙O交AB于C.
如图,在△ABD中,∠A=∠B=30°,以AB边上一点O为圆心,过A,D两点作⊙O交AB于C.