题目内容
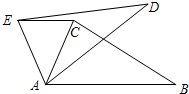 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A、30° | B、35° |
| C、40° | D、50° |
考点:旋转的性质
专题:
分析:根据两直线平行,内错角相等可得∠ACB=∠CAB,根据旋转的性质可得AC=AE,∠BAC=∠DAE,再根据等腰三角形两底角相等列式求出∠CAE,然后求出∠DAB=∠CAE,从而得解.
解答:解:∵CE∥AB,
∴∠ACB=∠CAB=75°,
∵△ABC绕点A逆时针旋转到△AED,
∴AC=AE,∠BAC=∠DAE,
∴∠CAE=180°-70°×2=40°,
∵∠CAE+∠CAD=∠DAE,
∠DAB+∠CAD=∠BAC,
∴∠DAB=∠CAE=40°.
故选C.
∴∠ACB=∠CAB=75°,
∵△ABC绕点A逆时针旋转到△AED,
∴AC=AE,∠BAC=∠DAE,
∴∠CAE=180°-70°×2=40°,
∵∠CAE+∠CAD=∠DAE,
∠DAB+∠CAD=∠BAC,
∴∠DAB=∠CAE=40°.
故选C.
点评:本题考查了旋转的性质,平行线的性质,等腰三角形两底角相等的性质,熟记各性质并求出∠DAB=∠CAE是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )
如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )A、
| ||
| B、11cm | ||
| C、13cm | ||
| D、17cm |
若关于x的方程
=3+
无解,则m的值是( )
| x+1 |
| x-2 |
| m-1 |
| 2-x |
| A、-2 | B、2 | C、1 | D、-4 |
若x、y为非负实数,且方程组
有解,则a的值为( )
|
| A、0 | B、-2 | C、2 | D、不定 |
 如图,在正八边形ABCDEFGH中,若四边形BCFG的面积是12cm2,则正八边形的面积为
如图,在正八边形ABCDEFGH中,若四边形BCFG的面积是12cm2,则正八边形的面积为 如图,在直角梯形ABCD中,BF=AE=DG=x,AB=6,CD=3,AD=4,则四边形CGEF的面积y与x之间的函数关系式为
如图,在直角梯形ABCD中,BF=AE=DG=x,AB=6,CD=3,AD=4,则四边形CGEF的面积y与x之间的函数关系式为