题目内容
3.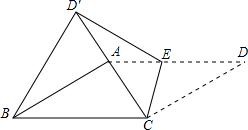 如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为D′,连接D′B,若△D′BC为等边三角形,则DE=2$\sqrt{3}$-2或$\sqrt{3}$+1.
如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为D′,连接D′B,若△D′BC为等边三角形,则DE=2$\sqrt{3}$-2或$\sqrt{3}$+1.
分析 先根据菱形的性质可得:∠D=∠ABC=30°,∠BCD=150°,然后根据△D′BC为等边三角形,可得∠BCD′=60°,然后根据折叠的性质可得:△DCE≌△D′CE,进而可得∠DCE=45°,然后过点E作EF⊥CD,垂足为F,然后解直角三角形DEF即可求出DE的值.
解答 解:①如图(1)所示,当点E在边AD上时,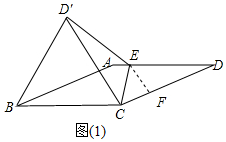
∵四边形ABCD是菱形,AB=2,∠ABC=30°,
∴CD=AB=2,∠D=∠A=30°,∠BCD=150°,
∵△D′BC为等边三角形,
∴∠BCD′=60°,
∴∠DCD′=90°,
∵△CDE沿CE折叠,得到△CD′E,
∴△DCE≌△D′CE,
∴∠DCE=$\frac{1}{2}∠$DCD′=45°,
过点E作EF⊥CD,垂足为F,
则∠CFE=90°,
∴∠CEF=∠DCE=45°,
∴CF=EF,
在Rt△DEF中,∠D=30°,
∴EF=$\frac{1}{2}$DE,
设EF=x,则DE=2x,CF=x,
由勾股定理可得:FD=$\sqrt{3}$x,
∵CF+FD=CD=2,
即x+$\sqrt{3}x$=2,
解得:x=$\sqrt{3}-1$,
∴DE=2x=2$\sqrt{3}$-2.
②当点E在DA的延长线上时,如图(2),过点B作BF⊥AD,交DA的延长线于点F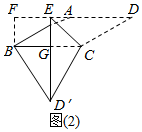
由折叠可知∠ED′C=∠D=30°,又∠BD′C=60°,所以D′E为∠BD′C的平分线
又△BD′C是等边三角形,所以D′E⊥BC.
又AD∥BC,所以D′E⊥AD
因为∠ABC=30°,所以∠BAF=30°
又AB=2,所以AD=$\sqrt{3}$,
令D′E与BC的交点为G,则易知EF=BG=$\frac{1}{2}$BC=1
所以AE=$\sqrt{3}$-1,
所以此时DE=$\sqrt{3}$+1.
故答案为:2$\sqrt{3}$-2或$\sqrt{3}$+1.
点评 此题考查了菱形的性质,折叠问题,解直角三角形及等边三角形的性质等知识,解题的关键是:添加辅助线,构造两个特殊的直角三角形,然后解直角三角形即可.

 口算能手系列答案
口算能手系列答案| A. | 12 | B. | 9 | C. | 13 | D. | 12或9 |
| A. | m≤3 | B. | m<3 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
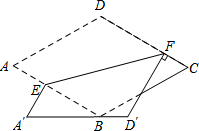 如图,边长为2的菱形纸片ABCD中,∠A=60°,将该纸片折叠,EF为折痕,点A、D分别落在A′、D′处.若A′D′经过点B,且D′F⊥CD,则DF的长为( )
如图,边长为2的菱形纸片ABCD中,∠A=60°,将该纸片折叠,EF为折痕,点A、D分别落在A′、D′处.若A′D′经过点B,且D′F⊥CD,则DF的长为( )| A. | 2$\sqrt{3}$-2 | B. | 4-2$\sqrt{3}$ | C. | $\frac{3-\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
| A. | 互余两角的和是90° | B. | 全等三角形的面积相等 | ||
| C. | 等边三角形是中心对称图形 | D. | 两直线平行,同旁内角互补 |
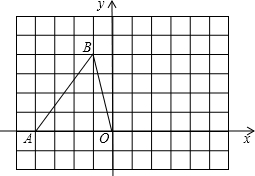 如图,在平面直角坐标系中,点A、B的坐标分别为A(-4,0),B(-1,4),将△AOB绕点O顺时针旋转90°
如图,在平面直角坐标系中,点A、B的坐标分别为A(-4,0),B(-1,4),将△AOB绕点O顺时针旋转90°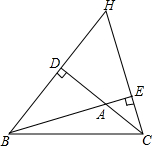 已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.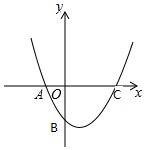 设抛物线y=$\frac{\sqrt{3}}{2}$(x+1)(x-2)与x轴交于A、C两点(点A在点C的左边),与y轴交于点B.
设抛物线y=$\frac{\sqrt{3}}{2}$(x+1)(x-2)与x轴交于A、C两点(点A在点C的左边),与y轴交于点B.