题目内容
8.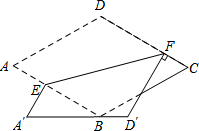 如图,边长为2的菱形纸片ABCD中,∠A=60°,将该纸片折叠,EF为折痕,点A、D分别落在A′、D′处.若A′D′经过点B,且D′F⊥CD,则DF的长为( )
如图,边长为2的菱形纸片ABCD中,∠A=60°,将该纸片折叠,EF为折痕,点A、D分别落在A′、D′处.若A′D′经过点B,且D′F⊥CD,则DF的长为( )| A. | 2$\sqrt{3}$-2 | B. | 4-2$\sqrt{3}$ | C. | $\frac{3-\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
分析 延长FC、A′D′相交于点G,根据菱形的对角相等求出∠BCD=∠A=60°,根据翻折的性质可得∠A′D′F=∠D,再求出∠FD′G=60°,根据直角三角形两锐角互余求出∠G=30°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CBG=30°,从而得到∠CBG=∠G,根据等角对等边求出BC=CG,然后利用∠G的正切值列式整理即可Q求出$\frac{FD}{FC}$的值,然后根据菱形的边长为2,即DF+FC=2,进而可求DF的值.
解答 解:如图,延长FC、A′D′相交于点G,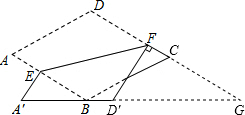 ∵菱形ABCD中,∠A=60°,
∵菱形ABCD中,∠A=60°,
∴∠BCD=∠A=60°,∠D=180°-60°=120°,
由翻折的性质得,∠A′D′F=∠D=120°,FD′=FD,
∴∠FD′G=180°-∠A′D′F=180°-120°=60°,
∵D′F⊥CD,
∴∠G=90°-∠FD′G=90°-60°=30°,
∴∠CBG=∠BCD-∠G=60°-30°=30°,
∴∠CBG=∠G,
∴BC=CG,
在Rt△FD′G中,tan∠G=$\frac{FD′}{FG}$,
∵FG=FC+CG=FC+BC=FC+CD=FC+FD+FC=2FC+FD,
∴tan30°=$\frac{FD}{2FC+FD}=\frac{\sqrt{3}}{3}$,
即$\frac{FD}{FC}=\sqrt{3}+1$,
∴FD=($\sqrt{3}+1$)FC,
∵FD+FC=2,
即($\sqrt{3}$+1)FC+FC=2,
解得:FC=4-2$\sqrt{3}$,
∴FD=2-FC=2$\sqrt{3}$-2.
故选A.
点评 本题考查了翻折变换的性质,菱形的性质,等腰三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,作辅助线构造出等腰三角形和直角三角形是解题的关键,也是本题的难点.

| A. | 精确到百分位,有3个有效数字 | B. | 精确到百分位,有5个有效数字 | ||
| C. | 精确到百位,有3个有效数字 | D. | 精确到百位,有5个有效数字 |
| A. | -1 | B. | 5 | C. | 1 或5 | D. | -1或5 |
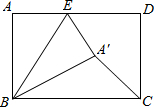 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )| A. | 3或4$\sqrt{2}$ | B. | 4或3$\sqrt{2}$ | C. | 3或4 | D. | 3$\sqrt{2}$或4$\sqrt{2}$ |
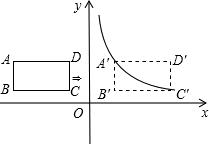 如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2.
如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2.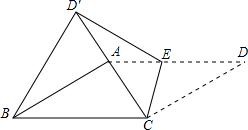 如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为D′,连接D′B,若△D′BC为等边三角形,则DE=2$\sqrt{3}$-2或$\sqrt{3}$+1.
如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为D′,连接D′B,若△D′BC为等边三角形,则DE=2$\sqrt{3}$-2或$\sqrt{3}$+1.