题目内容
已知sinA,sinB是方程4x2-2mx+m-1=0的两个实数根,且∠A,∠B是直角三角形的两个锐角,
(1)求m的值;
(2)求∠A和∠B的度数.
(1)求m的值;
(2)求∠A和∠B的度数.
考点:根与系数的关系,同角三角函数的关系,特殊角的三角函数值
专题:
分析:(1)由根与系数的关系得sinA+sinB=
,sinA•sinB=
,利用互余两角三角函数的关系得到sin2A+sin2B=1,变形得到(sinA+sinB)2-2sinA•sinB=1,所以(
)2-2×
=1,解得m1=1+
,m2=1-
,然后根据sinA与sinB都是正数确定m的取值;
(2)利用因式分解法求出已知方程的解得到x的值确定出sinA或sinB的值,即可求出∠A和∠B的度数.
| m |
| 2 |
| m-1 |
| 4 |
| m |
| 2 |
| m-1 |
| 4 |
| 3 |
| 3 |
(2)利用因式分解法求出已知方程的解得到x的值确定出sinA或sinB的值,即可求出∠A和∠B的度数.
解答:解:(1)根据题意得sinA+sinB=
,sinA•sinB=
,
∵sin2A+sin2B=1,
∴(sinA+sinB)2-2sinA•sinB=1,
∴(
)2-2×
=1,
解得m1=1+
,m2=1-
,
∵sinA+sinB=
>0,sinA•sinB=
>0,
∴m=1+
;
(2)当m=1+
时,方程即为4x2-2(1+
)x+
=0,
∴(2x-1)(2x-
)=0,
解得:x1=
,x2=
,
当sinA=
时,∠A=30°,则∠B=60°;
当sinB=
时,∠B=30°,则∠A=60°.
故∠A=30°或60°,∠B=60°或30°.
| m |
| 2 |
| m-1 |
| 4 |
∵sin2A+sin2B=1,
∴(sinA+sinB)2-2sinA•sinB=1,
∴(
| m |
| 2 |
| m-1 |
| 4 |
解得m1=1+
| 3 |
| 3 |
∵sinA+sinB=
| m |
| 2 |
| m-1 |
| 4 |
∴m=1+
| 3 |
(2)当m=1+
| 3 |
| 3 |
| 3 |
∴(2x-1)(2x-
| 3 |
解得:x1=
| 1 |
| 2 |
| ||
| 2 |
当sinA=
| 1 |
| 2 |
当sinB=
| 1 |
| 2 |
故∠A=30°或60°,∠B=60°或30°.
点评:本题考查了根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,则x1+x2=-
,x1x2=
.也考查了互余两角三角函数的关系,解一元二次方程-因式分解法.
| b |
| a |
| c |
| a |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
对抛物线y=2x2判断正确的是( )
| A、抛物线的开口向上 |
| B、抛物线的开口向下 |
| C、抛物线经过一、二、三象限 |
| D、抛物线经过二、三、四象限 |
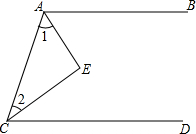 如图,AE、CE分别平分∠BAC和∠ACD,∠1和∠2互余,试说明AB∥CD.
如图,AE、CE分别平分∠BAC和∠ACD,∠1和∠2互余,试说明AB∥CD.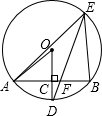 如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.