题目内容
18.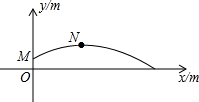 2015年10月22日,第一届全国青年运动会田径项目展开首金争夺,在男子铅球项目上,孙帅以20.39米的成绩力压群雄,摘得青年运动会田径项目首枚金牌.孙帅在赛后的一次投掷铅球的训练时,铅球经过的抛物线如图所示,其中出手点M的坐标为(0,$\frac{9}{5}$),铅球在最高点N的坐标为(9,$\frac{144}{35}$).(提示:$\sqrt{576}$=24)
2015年10月22日,第一届全国青年运动会田径项目展开首金争夺,在男子铅球项目上,孙帅以20.39米的成绩力压群雄,摘得青年运动会田径项目首枚金牌.孙帅在赛后的一次投掷铅球的训练时,铅球经过的抛物线如图所示,其中出手点M的坐标为(0,$\frac{9}{5}$),铅球在最高点N的坐标为(9,$\frac{144}{35}$).(提示:$\sqrt{576}$=24)(1)求该抛物线的解析式;
(2)试判断此次铅球落地时与点O的距离是否超过比赛中20.39米的成绩;
(3)男子铅球世界纪录保持者是美国运动员巴尔斯,成绩为23.13米,若张帅某次训练成绩达到了23米,该次铅球抛物线的顶点坐标为(10,$\frac{144}{35}$),求出手点的高度.(结果保留两位小数)
分析 (1)根据题意设函数解析式为顶点式,然后根据M(0,$\frac{9}{5}$)在此抛物线上,可以求得此抛物线的解析式;
(2)将y=0代入y=-$\frac{1}{35}$(x-9)2+$\frac{144}{35}$,即可得到结论;
(3)设抛物线的解析式为:y=a(x-10)2+$\frac{144}{35}$,把(23,0)代入y=a(x-10)2+$\frac{144}{35}$,求得抛物线的解析式为:y=-$\frac{144}{5915}$(x-10)2+$\frac{144}{35}$,于是得到结论.
解答 解:(1)设抛物线的解析式为:y= a(x-9)2+$\frac{144}{35}$,
a(x-9)2+$\frac{144}{35}$,
∵M(0,$\frac{9}{5}$)在此抛物线上,
∴$\frac{9}{5}$=a(0-9)2+$\frac{144}{35}$,
∴a=-$\frac{1}{35}$,
即抛物线的解析式是:y=-$\frac{1}{35}$(x-9)2+$\frac{144}{35}$;
(2)将y=0代入y=-$\frac{1}{35}$(x-9)2+$\frac{144}{35}$,
解得x1=-3,x2=21,
∵掷出的距离为正值,
∴孙帅掷出的距离是21米>20.39米,
即超过比赛中20.39米的成绩;
(3)设抛物线的解析式为:y=a(x-10)2+$\frac{144}{35}$,
把(23,0)代入y=a(x-10)2+$\frac{144}{35}$,
解得:a=-$\frac{144}{5915}$,
∴抛物线的解析式为:y=-$\frac{144}{5915}$(x-10)2+$\frac{144}{35}$,
当x=0时,y=1,70,
∴出手点的高度是1.70m.
点评 本题考查二次函数的应用,解题的关键是由题意可以列出相应的函数解析式,并且可以求出相应的函数解析式,根据题目要求巧妙的利用函数解析式解答问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案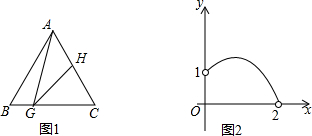 如图1,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B、C重合,H是AC边上一点,且∠AGH=30°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的( )
如图1,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B、C重合,H是AC边上一点,且∠AGH=30°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的( )| A. | 线段CG | B. | 线段AG | C. | 线段AH | D. | 线段CH |
| A. | 1或4 | B. | 1或-4 | C. | -1或-4 | D. | -1或4 |

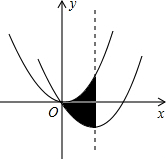 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}x$2经过平移得到抛物线y=$\frac{1}{2}{x}^{2}$-3x,其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{27}{2}$.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}x$2经过平移得到抛物线y=$\frac{1}{2}{x}^{2}$-3x,其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{27}{2}$. 图甲是由若干个小正方体搭成的几何体的俯视图,小正方体中的数字表示在该位置的小正方体的个数,那么这个几何体的主视图是( )
图甲是由若干个小正方体搭成的几何体的俯视图,小正方体中的数字表示在该位置的小正方体的个数,那么这个几何体的主视图是( )


