题目内容
13.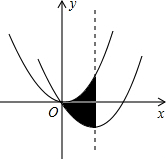 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}x$2经过平移得到抛物线y=$\frac{1}{2}{x}^{2}$-3x,其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{27}{2}$.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}x$2经过平移得到抛物线y=$\frac{1}{2}{x}^{2}$-3x,其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{27}{2}$.
分析 确定出抛物线y=$\frac{1}{2}$x2-3x的顶点坐标,然后求出抛物线的对称轴与原抛物线的交点坐标,从而判断出阴影部分的面积等于三角形的面积,再根据三角形的面积公式列式计算即可得解.
解答 解:如图,∵y=$\frac{1}{2}$x2-3x=$\frac{1}{2}$(x-3)2-$\frac{9}{2}$,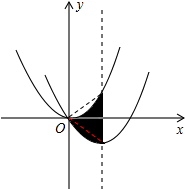
∴平移后抛物线的顶点坐标为(3,-$\frac{9}{2}$),对称轴为直线x=3,
当x=3时,y=$\frac{1}{2}$×32=$\frac{9}{2}$,
∴平移后阴影部分的面积等于如图三角形的面积,
$\frac{1}{2}$×($\frac{9}{2}$+$\frac{9}{2}$)×3=$\frac{27}{2}$.
故答案为:$\frac{27}{2}$.
点评 本题考查了二次函数图象与几何变换,确定出与阴影部分面积相等的三角形是解题的关键.

练习册系列答案
相关题目
3.不等式组$\left\{\begin{array}{l}{x+1<3}\\{\frac{3x+3}{2}>x}\end{array}\right.$的整数解的个数是( )
| A. | 无数个 | B. | 6 | C. | 5 | D. | 4 |
1.在下列各式中,3$\sqrt{2}$的同类二次根式是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\sqrt{20}$ |
8.下列调查中,适宜采用普查方式的是( )
| A. | 了解某校初三一班的体育学考成绩 | B. | 了解某种节能灯的使用寿命 | ||
| C. | 了解我国青年人喜欢的电视节目 | D. | 了解全国九年级学生身高的现状 |
5.若正比例函数y=kx与y=2x的图象关于x轴对称,则k的值等于( )
| A. | $\frac{1}{2}$ | B. | -2 | C. | -$\frac{1}{2}$ | D. | 2 |
3.二零一五年我国与“一带一路”国家贸易额达9955亿美元.数据9955用科学记数法表示为( )
| A. | 99.55×102 | B. | 9.955×103 | C. | 9.9×103 | D. | 10×103 |
 已知:当x>0时,反比例函数${y_1}=\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.
已知:当x>0时,反比例函数${y_1}=\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A、B.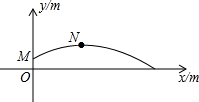 2015年10月22日,第一届全国青年运动会田径项目展开首金争夺,在男子铅球项目上,孙帅以20.39米的成绩力压群雄,摘得青年运动会田径项目首枚金牌.孙帅在赛后的一次投掷铅球的训练时,铅球经过的抛物线如图所示,其中出手点M的坐标为(0,$\frac{9}{5}$),铅球在最高点N的坐标为(9,$\frac{144}{35}$).(提示:$\sqrt{576}$=24)
2015年10月22日,第一届全国青年运动会田径项目展开首金争夺,在男子铅球项目上,孙帅以20.39米的成绩力压群雄,摘得青年运动会田径项目首枚金牌.孙帅在赛后的一次投掷铅球的训练时,铅球经过的抛物线如图所示,其中出手点M的坐标为(0,$\frac{9}{5}$),铅球在最高点N的坐标为(9,$\frac{144}{35}$).(提示:$\sqrt{576}$=24)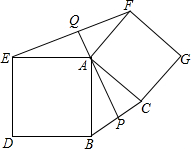 如图,两个正方形ABDE和ACGF,点P为BC中点,连接PA交EF于点Q,试探究AP与EF的数量和位置关系,并证明你的结论.
如图,两个正方形ABDE和ACGF,点P为BC中点,连接PA交EF于点Q,试探究AP与EF的数量和位置关系,并证明你的结论.