题目内容
8.关于x的一元二次方程(m-2)x2+(2m+1)x+m-2=0有两个不相等的正实数根,则m的取值范围是$\frac{3}{4}$<m<2.分析 设一元二次方程的两个根分别为x1,x2,根据方程有两个不相等的实数根可得出△>0,x1+x2>0,x1•x2>0,由此可得出m的取值范围.
解答 解:设一元二次方程的两个根分别为x1,x2,
∵关于x的一元二次方程(m-2)x2+(2m+1)x+m-2=0有两个不相等的正实数根,
∴△>0,x1+x2>0,x1•x2>0,
∴$\left\{\begin{array}{l}△=(2m+1)^{2}-4(m-2)^{2}>0①\\{x}_{1}+{x}_{2}=-\frac{2m+1}{m-2}>0②\\{x}_{1}•{x}_{2}=\frac{m-2}{m-2}>0\end{array}\right.$,
由①得m>$\frac{3}{4}$,
由②得-$\frac{1}{2}$<m<2.
故m的取值范围是:$\frac{3}{4}$<m<2.
故答案为:$\frac{3}{4}$<m<2.
点评 本题考查的是根的判别式,根据题意列出关于x的不等式组是解答此题的关键.

练习册系列答案
相关题目
3.二零一五年我国与“一带一路”国家贸易额达9955亿美元.数据9955用科学记数法表示为( )
| A. | 99.55×102 | B. | 9.955×103 | C. | 9.9×103 | D. | 10×103 |
13.己知x=3是关于x的方程x2+kx-6=0的一个根,则另一个根是( )
| A. | x=1 | B. | x=-2 | C. | x=-1 | D. | x=2 |
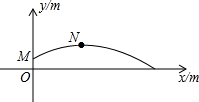 2015年10月22日,第一届全国青年运动会田径项目展开首金争夺,在男子铅球项目上,孙帅以20.39米的成绩力压群雄,摘得青年运动会田径项目首枚金牌.孙帅在赛后的一次投掷铅球的训练时,铅球经过的抛物线如图所示,其中出手点M的坐标为(0,$\frac{9}{5}$),铅球在最高点N的坐标为(9,$\frac{144}{35}$).(提示:$\sqrt{576}$=24)
2015年10月22日,第一届全国青年运动会田径项目展开首金争夺,在男子铅球项目上,孙帅以20.39米的成绩力压群雄,摘得青年运动会田径项目首枚金牌.孙帅在赛后的一次投掷铅球的训练时,铅球经过的抛物线如图所示,其中出手点M的坐标为(0,$\frac{9}{5}$),铅球在最高点N的坐标为(9,$\frac{144}{35}$).(提示:$\sqrt{576}$=24)