题目内容
14．
如图，四边形ABCD为⊙O的内接四边形，若∠BOD=90°，则∠BCD的大小为（ ）| A． | 90° | B． | 125° | C． | 135° | D． | 145° |
分析 根据圆周角定理求出∠A的度数，根据圆内接四边形的性质计算即可．
解答 解：∵∠BOD=90°，
∴∠A=$\frac{1}{2}$∠BOD=45°，
∵四边形ABCD为⊙O的内接四边形，
∴∠A+∠BCD=180°，
∴∠BCD=135°，
故选：C．
点评 本题考查的是圆内接四边形的性质和圆周角定理，掌握圆内接四边形的对角互补是解题的关键．
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目
2．
如图，圆内接四边形ABCD的两组对边的延长线分别相较于点E，F，若∠A=55°，∠E=30°，则∠F=（ ）
如图，圆内接四边形ABCD的两组对边的延长线分别相较于点E，F，若∠A=55°，∠E=30°，则∠F=（ ）| A． | 25° | B． | 30° | C． | 40° | D． | 55° |
9．谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注，人工智能完胜李世石，某教学网站开设了有关人工智能的课程并策划了A，B两种网上学习的月收费方式：
设小明每月上网学习人工智能课程的时间为x小时，方案A，B的收费金额分别为yA元，yB元．
（1）当x≥50时，分别求出yA，yB与x之间的函数关系式；
（2）若小明3月份上该网站学习的时间为60小时，则他选择哪种方式上网学习合算？
| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/（元/min） |
| A | 7 | 25 | 0.6 |
| B | 10 | 50 | 0.8 |
（1）当x≥50时，分别求出yA，yB与x之间的函数关系式；
（2）若小明3月份上该网站学习的时间为60小时，则他选择哪种方式上网学习合算？
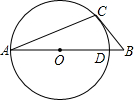如图，AC是⊙O的弦，CB是⊙O的切线，C为切点，AB经过圆心与⊙O的交点为D，若∠B=50°，AD=10，则$\widehat{CD}$的长为$\frac{10}{9}$π．（结果保留π）
6．在平面直角坐标系中，点M（-2，6）关于原点对称的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
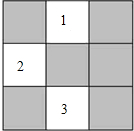某班级新做的表册栏被分割成如图所示的9个小长方形区域，标有标号1、2、3的3个小方格区域的可粘贴新内容，另外6个小方格需要保留，除此以外小方格完全相同．
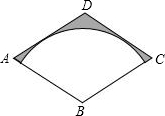如图，菱形ABCD的对角线BD、AC的长分别为2，2$\sqrt{3}$，以点B为圆心的弧与AD、DC相切，则图中阴影部分的面积是2$\sqrt{3}$-π．