题目内容
3.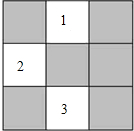 某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.
某班级新做的表册栏被分割成如图所示的9个小长方形区域,标有标号1、2、3的3个小方格区域的可粘贴新内容,另外6个小方格需要保留,除此以外小方格完全相同.(1)粗心的小明将一份通知随意地粘贴在图中所示的9个方格中的某一处上,求小明将这份通知粘贴在需保留区域小方格的概率;
(2)小伟准备从图中所示的标有编号1、2、3的3个小方格区域任意选取2个来粘贴课外活动表,则编号为1、2的两个小方格被粘贴的概率是多少?(用树状图或列表法求解)
分析 (1)由共有9个方格,需保留区域小方格有6个,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与编号为1、2的两个小方格被粘贴的情况,再利用概率公式即可求得答案.
解答 解:(1)∵共有9个方格,需保留区域小方格有6个,
∴小明将这份通知粘贴在需保留区域小方格的概率为:$\frac{6}{9}$=$\frac{2}{3}$;
(2)画树状图得: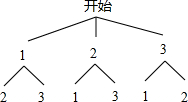
∵共有6种等可能的结果,编号为1、2的两个小方格被粘贴的有2种情况,
∴编号为1、2的两个小方格被粘贴的概率是:$\frac{2}{6}$=$\frac{1}{3}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )
如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )
 如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )
如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )| A. | 90° | B. | 125° | C. | 135° | D. | 145° |
8.与-2的和为0的数是( )
| A. | 2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -2 |
 如图,D,E,F分别是三角形ABC各边的中点,AG是高,如果ED=5,那么GF的长为5.
如图,D,E,F分别是三角形ABC各边的中点,AG是高,如果ED=5,那么GF的长为5. 如图,△ABC中,∠ACB=90°,tanA=$\frac{4}{3}$,AB=15,AC=9.
如图,△ABC中,∠ACB=90°,tanA=$\frac{4}{3}$,AB=15,AC=9. 如图,抛物线C1是二次函数y=x2-10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;它与x轴的另一交点为A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…,若某段抛物线上有一点
如图,抛物线C1是二次函数y=x2-10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;它与x轴的另一交点为A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…,若某段抛物线上有一点 如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且
如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且 己知常数a(a是常数)满足下面两个条件:
己知常数a(a是常数)满足下面两个条件: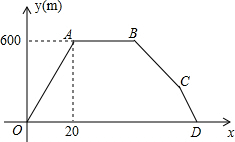 某山山脚的M处到山顶的N处有一条长为600米的登山路,小李沿此路从M走到N,停留后再原路返回,期间小李离开M处的路程y米与离开M处的时间x分(x>0)之间的函数关系如图中折线OABCD所示.
某山山脚的M处到山顶的N处有一条长为600米的登山路,小李沿此路从M走到N,停留后再原路返回,期间小李离开M处的路程y米与离开M处的时间x分(x>0)之间的函数关系如图中折线OABCD所示.