题目内容
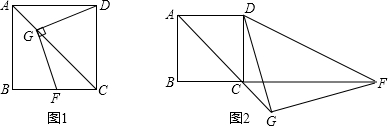
1.如图1,正方形ABCD中,点G是直线AC上一点.(1)GF⊥DG交BC于点F,求证:GD=GF;
(2)如图2,点F在BC的延长线上,且GD=GF,求证:∠GDC=∠GFC;
(3)在(2)的条件下,若在线段AC上存在点G,使∠AGD=3∠GFC,直接写出$\frac{CG}{AG}$=$\sqrt{2}$-1.
分析 (1)连接BG,由正方形的对称性得出△ABG≌△ADG,得出GB=GD,∠1=∠2,证出∠3=∠4,由等角对等边得出GB=GF,即可得出结论;
(2)连接BG,同(1)得:△BCG≌△DCG,得出GB=GD,∠GBC=∠GDC,由已知条件得出GB=GF,由等腰三角形的性质得出∠GBC=∠GFC,即可得出结论;
(3)连接BG,由(2)得:△ABG≌△ADG,GB=GD=GF,得出∠AGB=∠AGD=3∠GFC,∠GBC=∠GFC,设∠GBC=∠GFC=x,则∠AGB=∠AGD=3∠GFC=3x,由三角形的外角性质得出∠BCG=2x=45°,得出x=22.5°,∠AGB=∠ABG,由等角对等边证出AG=AB,由AC=$\sqrt{2}$AB=$\sqrt{2}$AG,即可得出结果.
解答 (1)证明:连接BG,如图1所示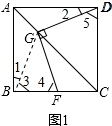
∵四边形ABCD是正方形,
∴∠ABC=∠ADC=∠BCD=90°,正方形ABCD关于直线AC对称,
∴△ABG≌△ADG,
∴GB=GD,∠1=∠2,
∴∠3=∠5,
∵GF⊥DG,
∴∠DGF=90°,
∴∠GFC+∠5=180°,
∵∠4+∠GFC=180°,
∴∠4=∠5,
∴∠3=∠4,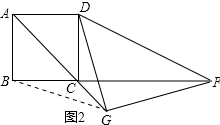
∴GB=GF,
∴GD=GF;
(2)证明:连接BG,如图所示:
同(1)得:△BCG≌△DCG,
∴GB=GD,∠GBC=∠GDC,
∵GD=GF,
∴GB=GF,
∴∠GBC=∠GFC,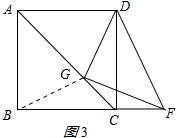
∴∠GDC=∠GFC;
(3)解:如图所示:连接BG,
由(2)得:△ABG≌△ADG,GD=GF,
∴GB=GD=GF,∠AGB=∠AGD=3∠GFC,
∴∠GBC=∠GFC,
设∠GBC=∠GFC=x,
则∠AGB=∠AGD=3∠GFC=3x,
∵∠AGB=∠GBC+∠BCG,
∴∠BCG=2x=45°,
∴x=22.5°,
∴∠AGB=3×22.5°=67.5°,∠ABG=90°-22.5°=67.5°,
∴∠AGB=∠ABG,
∴AG=AB,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴AC=$\sqrt{2}$AB=$\sqrt{2}$AG,
∴$\frac{CG}{AG}$=$\frac{AC-AG}{AG}$=$\frac{\sqrt{2}AG-AG}{AG}$=$\sqrt{2}$-1,
故答案为:$\sqrt{2}$-1.
点评 本题考查了正方形的性质、等腰三角形的判定与性质、三角形的外角性质、等腰直角三角形的性质、勾股定理等知识;本题综合性强,有一定难度,需要通过作辅助线由正方形的对称性得出等腰三角形是解决问题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 3 | B. | 6 | C. | 3或6 | D. | 4或5 |
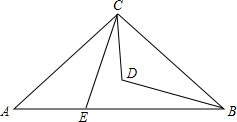 如图,在△ABC中,∠ACB=90°,AC=BC,CD平分∠ACB,E为AB边上一点,且∠ACE=∠CBD,求证:AE=CD.
如图,在△ABC中,∠ACB=90°,AC=BC,CD平分∠ACB,E为AB边上一点,且∠ACE=∠CBD,求证:AE=CD.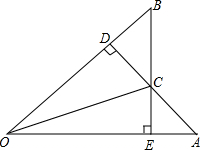 如图,AE=BD,AD⊥OB于点D,BE⊥OA于点E,AD、BE交于点C.连OC,求证:OC平分∠AOB.
如图,AE=BD,AD⊥OB于点D,BE⊥OA于点E,AD、BE交于点C.连OC,求证:OC平分∠AOB.