题目内容
13.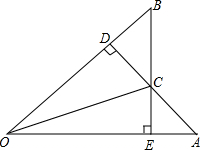 如图,AE=BD,AD⊥OB于点D,BE⊥OA于点E,AD、BE交于点C.连OC,求证:OC平分∠AOB.
如图,AE=BD,AD⊥OB于点D,BE⊥OA于点E,AD、BE交于点C.连OC,求证:OC平分∠AOB.
分析 根据垂直的定义得到∠BDC=∠AEC=90°,推出△BDC≌△AEC,根据全等三角形的性质得到CD=CE,由角平分线的判定即可得到结论.
解答 证明:∵AD⊥OB于点D,BE⊥OA于点E,
∴∠BDC=∠AEC=90°,
在△BDC与△AEC中,$\left\{\begin{array}{l}{∠BDC=∠AEC}\\{∠BCD=∠ACE}\\{BD=AE}\end{array}\right.$,
∴△BDC≌△AEC,
∴CD=CE,
∴OC平分∠AOB.
点评 此题主要考查了全等三角形的判定与性质,角平分线的判定定理,根据题意熟练利用全等三角形的判定定理是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列方程中,是一元一次方程的是( )
| A. | x2-4x=3 | B. | y=-2 | C. | x+2y=1 | D. | x-1=$\frac{1}{x}$ |
5.以下列各组长度的线段为边,能构成三角形的是( )
| A. | 7,3,4 | B. | 5,6,12 | C. | 3,4,5 | D. | 1,2,3 |
18.设a为实数且0<a<1,则在a2,a,$\sqrt{a}$,$\frac{1}{a}$这四个数中( )
| A. | $\frac{1}{a}>a>\sqrt{a}>{a}^{2}$ | B. | ${a}^{2}>a>\sqrt{a}>\frac{1}{a}$ | C. | $\sqrt{a}>a>\frac{1}{a}>{a}^{2}$ | D. | $\frac{1}{a}>\sqrt{a}>a>{a}^{2}$ |
3.将多项式-y2+2y3+1-y按照字母y升幂排列正确的是( )
| A. | 2y3-y2-y+1 | B. | -y-y2+2y3+1 | C. | 1+2y3-y2-y | D. | 1-y-y2+2y3 |
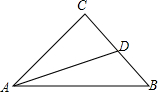 已知:CA=CB,AD平分∠CAB,且AB=AC+CD,求证:AC⊥BC.
已知:CA=CB,AD平分∠CAB,且AB=AC+CD,求证:AC⊥BC.