Question

12．根据指令[s，A]（s≥0，0°＜A＜180°），机器人在平面上能完成下列动作：先原地逆时针旋转角度A，再朝其面对的方向沿直线行走距离s，现机器人在直角坐标系的坐标原点，且面对x轴正方向，若下指令[4，60°]，则机器人应移动到点（2，2$\sqrt{3}$）．

Answer 1

分析 根据指令[4，60°]画出图形，如图，∠POx=60°，OP=4，作PQ⊥x轴于Q，利用∠POQ的正弦可计算出PQ=4sin60°=2$\sqrt{3}$，利用含30度的直角三角形三边的关系可得到OQ=$\frac{1}{2}$OP=2，所以P点坐标为（2，2$\sqrt{3}$）．

解答 解：如图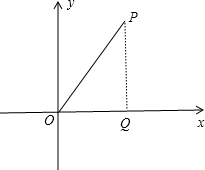，∠POx=60°，OP=4，
作PQ⊥x轴于Q，
在Rt△POQ中，∵sin∠POQ=$\frac{PQ}{OP}$，
∴PQ=4sin60°=2$\sqrt{3}$，
而OQ=$\frac{1}{2}$OP=2，
∴P点坐标为（2，2$\sqrt{3}$），
即机器人应移动到点（2，2$\sqrt{3}$）．
故答案为（2，2$\sqrt{3}$）．

点评 本题考查了坐标与图形变化-旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．解决本题的关键是根据新定义画出几何图形．