题目内容
6.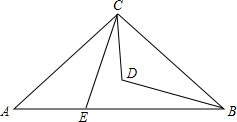 如图,在△ABC中,∠ACB=90°,AC=BC,CD平分∠ACB,E为AB边上一点,且∠ACE=∠CBD,求证:AE=CD.
如图,在△ABC中,∠ACB=90°,AC=BC,CD平分∠ACB,E为AB边上一点,且∠ACE=∠CBD,求证:AE=CD.
分析 根据等腰直角三角形的性质和角平分线的定义得到∠A=∠BCD,推出△ACE≌△BCD,根据全等三角形的性质即可得到结论.
解答 证明:∵∠ACB=90°,AC=BC,
∴∠A=45°,
∵CD平分∠ACB,
∴∠BCD=$\frac{1}{2}∠$ACB=45°,
∴∠A=∠BCD,
在△ACE与△BCD中,$\left\{\begin{array}{l}{∠A=∠BCD}\\{AC=BC}\\{∠ACE=∠BCD}\end{array}\right.$,
∴△ACE≌△BCD,
∴AE=CD.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,角平分线的定义,熟记全等三角形的判定定理是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
18.设a为实数且0<a<1,则在a2,a,$\sqrt{a}$,$\frac{1}{a}$这四个数中( )
| A. | $\frac{1}{a}>a>\sqrt{a}>{a}^{2}$ | B. | ${a}^{2}>a>\sqrt{a}>\frac{1}{a}$ | C. | $\sqrt{a}>a>\frac{1}{a}>{a}^{2}$ | D. | $\frac{1}{a}>\sqrt{a}>a>{a}^{2}$ |
15.下列语句中,正确的有( )
| A. | 圆是轴对称图形,任何一条直径都是它的对称轴 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 在同圆或等圆中,相等的圆心角所对的弧相等 | |
| D. | 长度相等的两条弧相等 |