题目内容
18.使$\sqrt{2-x}$有意义的x的取值范围是x≤2,使分式$\frac{x-3}{x+2}$的值为零的x的值是x=3.
分析 根据被开方数是非负数,可得答案;
根据分母不为零分式有意义,分子为零分式的值为零,可得答案.
解答 解:由$\sqrt{2-x}$有意义,得
2-x≥0,
解得x≤2;
由分式$\frac{x-3}{x+2}$的值为零,得
x-3=0且x+2≠0.
解得x=3,
故答案为:x≤2,x=3.
点评 本题考查了二次根式有意义的条件,被开方数是非负数是解题关键.

练习册系列答案
相关题目
3.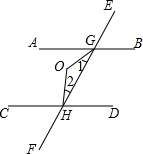 如图,直线AB∥CD,EF分别与AB、CD交于G、H,若∠1=$\frac{1}{3}∠AGH,∠2=\frac{1}{3}$∠CHG,则∠GOH的度数为( )
如图,直线AB∥CD,EF分别与AB、CD交于G、H,若∠1=$\frac{1}{3}∠AGH,∠2=\frac{1}{3}$∠CHG,则∠GOH的度数为( )
 如图,直线AB∥CD,EF分别与AB、CD交于G、H,若∠1=$\frac{1}{3}∠AGH,∠2=\frac{1}{3}$∠CHG,则∠GOH的度数为( )
如图,直线AB∥CD,EF分别与AB、CD交于G、H,若∠1=$\frac{1}{3}∠AGH,∠2=\frac{1}{3}$∠CHG,则∠GOH的度数为( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
 已知△ABC,求作:AC边上的高.
已知△ABC,求作:AC边上的高.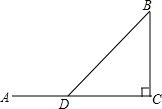 如图,已知△ABC中,∠C=90°.
如图,已知△ABC中,∠C=90°.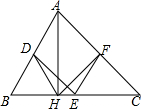 已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.
已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.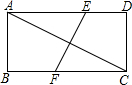 如图,矩形ABCD中,AB=2,AD=4,AC的垂直平分线EF交AD于点E,交BC于点F,则DE=$\frac{3}{2}$.
如图,矩形ABCD中,AB=2,AD=4,AC的垂直平分线EF交AD于点E,交BC于点F,则DE=$\frac{3}{2}$.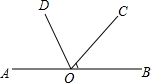 如图,点O在直线AB上,∠BOC=40°,OD平分∠AOC,求∠BOD的度数.
如图,点O在直线AB上,∠BOC=40°,OD平分∠AOC,求∠BOD的度数.