题目内容
6.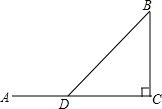 如图,已知△ABC中,∠C=90°.
如图,已知△ABC中,∠C=90°.(1)用直尺和圆规在△ABC所在的平面内找一点P,使PA=PB=PC.
(2)如果∠B=30°,AC=2,求△ABC的面积.
分析 (1)作BC的垂直平分线交斜边AB于点P,则点P满足条件;
(2)利用含30度的直角三角形三边的关系求出BC,然后根据三角形面积公式求解.
解答 解:(1)如图,点P为所作;
(2)∵∠B=30°,
∴BC=$\sqrt{3}$AC=2$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$.
点评 本题考查了基本作图:作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.

练习册系列答案
相关题目
1.下列各式计算正确的是( )
| A. | $\sqrt{2}+\sqrt{5}=\sqrt{7}$ | B. | $3\sqrt{2}-\sqrt{2}=3$ | C. | $\frac{\sqrt{2}}{\sqrt{5}}$=5$\sqrt{10}$ | D. | $\sqrt{2}$$•\sqrt{5}$=$\sqrt{10}$ |
11.在解方程$\frac{x-1}{2}$-$\frac{2x+1}{3}$=1时,去分母正确的是( )
| A. | 3(x-1)-2(2x+3)=6 | B. | 3x-3-4x+3=1 | C. | 3(x-1)-2(2x+3)=1 | D. | 3x-3-4x-2=6 |
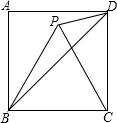 如图,四边形ABCD为正方形,△BPC为等边三角形,连接PD、BD,则∠BDP=30°.
如图,四边形ABCD为正方形,△BPC为等边三角形,连接PD、BD,则∠BDP=30°.