题目内容
13.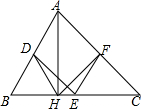 已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.
已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.(1)求证:DH=EF;
(2)求证:∠DHF=∠DEF.
分析 (1)根据三角形中位线定理得到EF=$\frac{1}{2}$AB,根据直角三角形的性质得到DH=$\frac{1}{2}$AB,证明结论;
(2)连接DF,证明△DHF≌△DEF,证明结论.
解答 证明:(1)∵E、F分别是边BC、AC的中点,
∴EF=$\frac{1}{2}$AB,
∵AH⊥BC,D是AB的中点,
∴DH=$\frac{1}{2}$AB,
∴DH=EF;
(2)连接DF,
由(1)得,DH=EF,
同理DE=HF,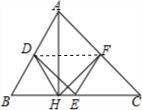
在△DHF和△DEF中,
$\left\{\begin{array}{l}{DH=FE}\\{HF=ED}\\{DF=FD}\end{array}\right.$,
∴△DHF≌△DEF,
∴∠DHF=∠DEF.
点评 本题考查的是直角三角形的性质、全等三角形的判定和性质,掌握直角三角形中,斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
3.下列计算:①0-(-5)=0+(-5)=-5;②5-3×4=5-12=-7;③4÷3×(-$\frac{1}{3}$)=4÷(-1)=-4;④-12-2×(-1)2=1+2=3.其中错误的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.下列各式计算正确的是( )
| A. | $\sqrt{2}+\sqrt{5}=\sqrt{7}$ | B. | $3\sqrt{2}-\sqrt{2}=3$ | C. | $\frac{\sqrt{2}}{\sqrt{5}}$=5$\sqrt{10}$ | D. | $\sqrt{2}$$•\sqrt{5}$=$\sqrt{10}$ |
3.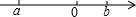 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )
实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )
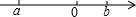 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )
实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )| A. | 2a+b | B. | 2a-b | C. | -2a+b | D. | b |
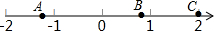 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m.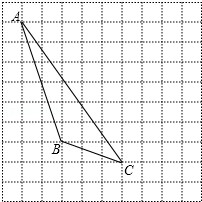 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.