题目内容
10．
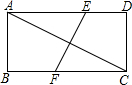如图，矩形ABCD中，AB=2，AD=4，AC的垂直平分线EF交AD于点E，交BC于点F，则DE=$\frac{3}{2}$．
分析 利用线段垂直平分线的性质得出AE=EC，再利用勾股定理求出答案．
解答 
解：连接EC，
∵矩形ABCD中，AB=2，
∴DC=2，
∵AC的垂直平分线EF交AD于点E，
∴AE=EC，
设AE=EC=x，则ED=4-x，
故x2=（4-x）2+22，
解得：x=$\frac{5}{2}$，
故ED=4-$\frac{5}{2}$=$\frac{3}{2}$．
故答案为：$\frac{3}{2}$．
点评 此题主要考查了矩形的性质以及勾股定理和线段垂直平分线的性质等知识，正确构造直角三角形是解题关键．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
1．下列各式计算正确的是（ ）
| A． | $\sqrt{2}+\sqrt{5}=\sqrt{7}$ | B． | $3\sqrt{2}-\sqrt{2}=3$ | C． | $\frac{\sqrt{2}}{\sqrt{5}}$=5$\sqrt{10}$ | D． | $\sqrt{2}$$•\sqrt{5}$=$\sqrt{10}$ |
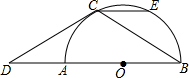如图，AB是半圆O的直径，点C在半圆上，过点C的切线交BA的延长线于点D，CD=CB，CE∥AB交半圆于点E．