题目内容
5．求二次根式$\sqrt{{m}^{2}-2mn+{n}^{2}}$的值，其中m=-2+$\sqrt{3}$，n=-2-$\sqrt{3}$．分析 直接利用完全平方公式因式分解进入二次根式的化简，然后代入求出答案即可．
解答 解：∵$\sqrt{{m}^{2}-2mn+{n}^{2}}$=$\sqrt{（m-n）^{2}}$=|m-n|，
当m=-2+$\sqrt{3}$，n=-2-$\sqrt{3}$时，
原式=2$\sqrt{3}$．
点评 此题主要考查了二次根式的化简求值，熟练应用完全平方公式是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在四边形ABCD中，对角线AC⊥BD且AC=6，BD=8，点E、F、G分别是边AB、CD、AD的中点，则EF=5．
13．
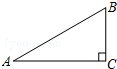在Rt△ABC中，∠C=90°，AB=2，BC=1，则sinB的值是（ ）
在Rt△ABC中，∠C=90°，AB=2，BC=1，则sinB的值是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 2 |
如图，两条平行线a、b被直线c所截．若∠1=40°，则∠2=140°．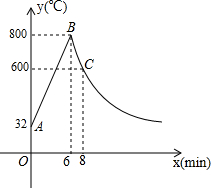
如图，制作某金属工具先将材料煅烧6分钟温度升到800℃，再停止煅烧进行锻造，8分钟温度降为600℃；煅烧时温度y（℃）与时间x（min）成一次函数关系；锻造时温度y（℃）与时间x（min）成反比例函数关系；该材料初始温度是32℃．