题目内容
13．
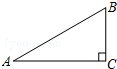在Rt△ABC中，∠C=90°，AB=2，BC=1，则sinB的值是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 2 |
分析 首先根据勾股定理求得AC的长，然后根据正弦的定义即可求解．
解答 解：根据勾股定理可得：AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{3}$，
∴sinB=$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$．
故选C．
点评 本题主要考查了正弦函数的定义，正确记忆定义是解题关键．
练习册系列答案
相关题目
阅读下列材料：阅读下列材料：
8．
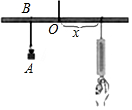如图所示，小华设计了一个研究杠杆平衡条件的实验，在一根长为1000cm的匀质木杆的中点左侧固定位置B处悬挂重物A，在中点的右侧用一个弹簧秤向下拉，改变弹簧与点O的距离x（cm）观察弹簧的示数y（N）的变化情况，实验数据记录如下：
（1）观察数据，求出y（N）与x（cm）之间的函数关系式，写出自变量的取值范围；
（2）当弹簧秤的示数是24N时，弹簧与点O的距离是多少？随着弹簧秤与点O的距离不断减小，弹簧秤上的示数将发生怎样的变化？
如图所示，小华设计了一个研究杠杆平衡条件的实验，在一根长为1000cm的匀质木杆的中点左侧固定位置B处悬挂重物A，在中点的右侧用一个弹簧秤向下拉，改变弹簧与点O的距离x（cm）观察弹簧的示数y（N）的变化情况，实验数据记录如下：| x（cm） | … | 10 | 15 | 20 | 25 | 30 | … |
| y（N） | … | 30 | 20 | 15 | 12 | 10 | … |
（2）当弹簧秤的示数是24N时，弹簧与点O的距离是多少？随着弹簧秤与点O的距离不断减小，弹簧秤上的示数将发生怎样的变化？
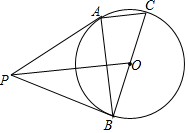如图，P为⊙O外一点，BC是⊙O的直径，CA为⊙O的一条弦，连接PA、PB，∠PBA=∠C．