题目内容

4．在式子$\frac{a+1}{3}$，-$\frac{2}{3}$abc，0，-a，x-y，$\frac{2}{x}$，$\frac{1}{π}$中，单项式的个数是（　　）
A．5个B．4个C．3个D．2个

分析 根据单项式的概念对各个式子进行判断即可．

解答 解：-$\frac{2}{3}$abc，0，-a，$\frac{1}{π}$是单项式，
故选：B．

点评 本题考查的是单项式的概念，数或字母的积组成的式子叫做单项式，单独的一个数或字母也是单项式．

练习册系列答案
相关题目
14．如图，在四边形ABCD中，AD∥BC，AD=12，CD=10，BC=20，高DE=8，点P从点A出发，沿A-D-A运动，点Q从点C出发，沿CB方向运动，速度均为每秒4个单位长度．P、Q两点同时出发，当点Q到达B点时，P、Q两点同时停止运动．设点P运动时间为t（秒），连接P、Q．
（1）当t=1时，AP=4；当t=4时，AP=8
（2）连接DQ，在整个运动过程中，当t为何值时，△DPQ的面积为24？
（3）设点C、D关于直线PQ的对称点分别为点C′、D′，直接写出C′D′∥BC时所有t的值．
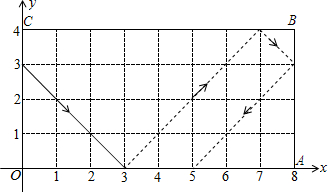15．如图，动点P从（0，3）出发，沿所示方向运动，每当碰到长方形OABC的边时反弹，反弹后的路径与长方形的边的夹角为45°，第1次碰到长方形边上的点的坐标为（3，0），则第3次碰到长方形边上的点的坐标为（8，3），第2015次碰到长方形边上的点的坐标为（1，4）．
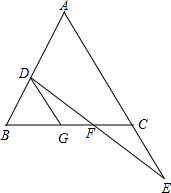12．如图：E在△ABC的AC边的延长线上，D点在AB边上，DE交BC于点F，DF=EF，BD=CE，过D作DG∥AC交BC于G．
（1）求证：△GDF≌△CEF；
（2）若AB=5，BC=6，求△ABC的面积．
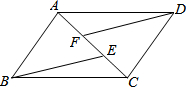19．如图，四边形ABCD中，AB∥CD，AB=CD，A、F、E、C在同一直线上，∠ABE=∠CDF．
（1）试说明：△ABE≌△CDF；
（2）试说明：AF=CE．
9．下列各数：-5，π，-$\frac{10}{3}$，-0.$\stackrel{..}{15}$，0，-（-2），-1.1010010001…，3.1415926中，
整数集合：{                                 …}
无理数集合：{                               …}．
16．（1）计算：6tan230°-$\sqrt{3}$sin60°-$\sqrt{2}$sin45°    
（2）先化简，再求值：$\frac{x}{{x}^{2}-1}$÷（1+$\frac{1}{x-1}$），其中x=$\sqrt{2}$-1．
13．问题提出：求边长分别为$\sqrt{4+{a}^{2}}$，$\sqrt{1+9{a}^{2}}$，$\sqrt{9+4{a}^{2}}$（a为正整数）三角形的面积．
  问题探究：为解决上述数学问题，我们采取数形结合和转化的思想方法，并采取一般问题特殊化的策略来进行探究．
  探究一：当a=1时，求边长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$三角形的面积．
  先画一个正方形网格（每个小正方形的边长为1），再在网格中画出边长分别为$\sqrt{5}$，$\sqrt{10}$，$\sqrt{13}$的格点三角形△ABC（如图①）．
  因为AB是直角边分别为2和1的Rt△ABE的斜边，所以AB=$\sqrt{5}$；
  因为BC是直角边分别为1和3的Rt△BCF的斜边，所以BC=$\sqrt{10}$；
  因为AC是直角边分别为3和2的Rt△ACG的斜边，所以AC=$\sqrt{13}$；通过面积转化，可间接求三角形△ABC的面积．
  所以，S△ABC=S正方形EFCG-S△ABE-S△BCF-S△ACG．

（1）直接写出图①中S△ABC=3.5．
  探究二：当a=2时，求边长分别为2$\sqrt{2}$，$\sqrt{37}$，5三角形的面积．
  先画一个长方形网格（每个小长方形的长为2，宽为1），再在网格中画出边长分别为2$\sqrt{2}$，$\sqrt{37}$，5的格点三角形△ABC（如图②）．
  因为AB是直角边分别为2和2的Rt△ABE的斜边，所以AB=2$\sqrt{2}$；
  因为BC是直角边分别为1和6的Rt△BCF的斜边，所以BC=$\sqrt{37}$；
  因为AC是直角边分别为3和4的Rt△ACG的斜边，所以AC=5，通过面积转化，可间接求三角形△ABC的面积．
  所以，S△ABC=S正方形EFCG-S△ABE-S△BCF-S△ACG
（2）直接写出图②中S△ABC=7．
  探究三：当a=3时，求边长分别为$\sqrt{13}$，$\sqrt{82}$，3$\sqrt{5}$三角形的面积．

  仿照上述方法解答下列问题：
（3）画的长方形网格中，每个小长方形的长应是2．
（4）边长分别为$\sqrt{13}$，$\sqrt{82}$，3$\sqrt{5}$的三角形的面积为$\frac{21}{2}$．
问题解决：求边长分别为$\sqrt{4+{a}^{2}}$，$\sqrt{1+9{a}^{2}}$，$\sqrt{9+4{a}^{2}}$（a为正整数）三角形的面积．
（5）类比上述方法画长方形网格，每个小长方形的长应是a．
（6）边长分别为$\sqrt{4+{a}^{2}}$，$\sqrt{1+9{a}^{2}}$，$\sqrt{9+4{a}^{2}}$（a为正整数）的三角形的面积是$\frac{7}{2}$a．
14．估计$\sqrt{89}$的大小应该在（　　）
A．7～8之间B．8～9之间C．9～9.5之间D．9.5～10之间

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网