题目内容
12.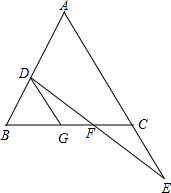 如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE,过D作DG∥AC交BC于G.
如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE,过D作DG∥AC交BC于G.(1)求证:△GDF≌△CEF;
(2)若AB=5,BC=6,求△ABC的面积.
分析 (1)利用平行线的性质得出∠GDF=∠CEF,进而利用ASA得出△GDF≌△CEF;
(2)由(1)△GDF≌△CEF得DG=CE,由于BD=CE,于是得到BD=DG,求得∠DBG=∠DGB,根据平行线的性质得到∠DGB=∠ACB,等量代换得到∠ABC=∠ACB,过A作AH⊥BC与H,根据等腰三角形的性质得到BH=$\frac{1}{2}$BC=3,由勾股定理得到AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=4,于是得到结论.
解答 证明:(1)∵DG∥AC,
∴∠GDF=∠CEF,
在△GDF和△CEF中,
$\left\{\begin{array}{l}{∠GDF=∠CEF}\\{DF=EF}\\{∠DFG=∠CFE}\end{array}\right.$,
∴△GDF≌△CEF(ASA);
(2)由(1)△GDF≌△CEF得DG=CE,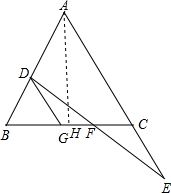
又∵BD=CE,
∴BD=DG,
∴∠DBG=∠DGB,
∵DG∥AC,
∴∠DGB=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC=5,
过A作AH⊥BC与H,
∴BH=$\frac{1}{2}$BC=3,
∴AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=4,
∴S△ABC=$\frac{1}{2}$BC•AH=$\frac{1}{2}×6×4$=12.
点评 本题考查了全等三角形的判定与性质,等腰三角形的判定和性质,勾股定理三角形的面积,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
4.在式子$\frac{a+1}{3}$,-$\frac{2}{3}$abc,0,-a,x-y,$\frac{2}{x}$,$\frac{1}{π}$中,单项式的个数是( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
1.下列计算正确的是( )
| A. | 3a2+a=4a3 | B. | -2(a-b)=-2a+b | C. | a2b-2a2b=-a2 b | D. | 5a-4a=1 |
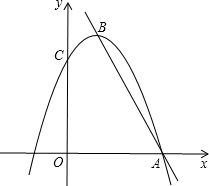 如图,在平面直角坐标系中xOy中,点O为坐标原点,直线y=-2x+6与x轴交于点A,点B(1,m)在直线y=-2x+6上.
如图,在平面直角坐标系中xOy中,点O为坐标原点,直线y=-2x+6与x轴交于点A,点B(1,m)在直线y=-2x+6上.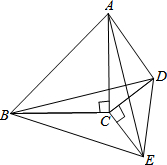 如图,在△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=90°,将△DCE绕点C旋转(0°<∠ACD<180°),连结BD和AE:
如图,在△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=90°,将△DCE绕点C旋转(0°<∠ACD<180°),连结BD和AE: