题目内容
4.(1)如图①,△ABC中,点D、E在边BC上,AE平分∠BAC,AD⊥BC,∠C=40°,∠B=60°,求:①∠CAE的度数;②∠DAE的度数.(2)如图②,若把(1)中的条件“AD⊥BC”变成“F为AE延长线上一点,且FD⊥BC”,其他条件不变,求出∠DFE的度数.
(3)在△ABC中,AE平分∠BAC,若F为EA延长线上一点,FD⊥BC,且∠C=α,∠B=β(β>α),试猜想∠DFE的度数(用α,β表示),请自己作出对应图形并说明理由.
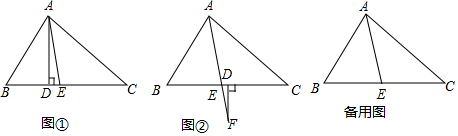
分析 (1)如图1中,求出∠BAD,∠BAE,根据∠DAE=∠BAE-∠BAD即可解决问题.
(2)如图2中,作AH⊥BC于H.利用(1)中结论,再证明∠DFE=∠HAE即可.
(3)结论:∠DFE=$\frac{1}{2}$(∠B-∠C).如图3中,作AH⊥BC于H,FD⊥BC于D.由∠HAE=∠EAB-∠BAH,∠BAH=90°-∠B,∠BAE=$\frac{1}{2}$(180°-∠B-∠C)推出∠HAE=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C-(90°-∠B)=$\frac{1}{2}$(∠B-∠C),由AH∥FD,推出∠DFE=∠HAE,即可解决问题.
解答 解:(1)如图(1).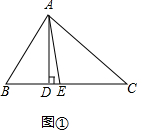
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°-∠B=90°-60°=30°,
∵∠BAC=180°-∠B-∠C=180°-60°-40°=80°,
而AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×80°=40°,
∴∠DAE=∠BAE-∠BAD=40°-30°=10°;
(2)如图2中,作AH⊥BC于H.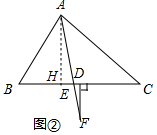
由(1)可知∠HAE=10°,
∵AH∥EF,
∴∠DFE=∠HAE=10°
(3)结论:∠DFE=$\frac{1}{2}$(∠B-∠C).理由如下:
如图3中,作AH⊥BC于H,FD⊥BC于D.
∵∠HAE=∠EAB-∠BAH,∠BAH=90°-∠B,∠BAE=$\frac{1}{2}$(180°-∠B-∠C),
∴∠HAE=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C-(90°-∠B)
=$\frac{1}{2}$(∠B-∠C),
∵AH∥FD,
∴∠DFE=∠HAE,
∴∠DFE=$\frac{1}{2}$(∠B-∠C).
点评 本题考查了三角形内角和定理:三角形内角和是180°.三角形内角和主要用在求三角形中角的度数.也考查了三角形外角性质.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案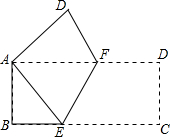 如图,将AB=4,BC=8的矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长是( )
如图,将AB=4,BC=8的矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长是( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
| 少分数段(x表示分数) | 频数 | 频率 |
| 50≤x<60 | 4 | 0.1 |
| 60≤x<70 | a | 0.2 |
| 70≤x<80 | 12 | b |
| 80≤x<90 | 10 | 0.25 |
| 90≤x<100 | 6 | 0.15 |

(1)表中a=8,b=0.3,并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段80≤x<100对应扇形的圆心角度数是144°;
(3)请估计该年级分数在60≤x<100的学生有多少人?
| A. | P(A)=1 | B. | P(A)=0 | C. | 0<P(A)<1 | D. | P(A)>1 |
| A. | 平均数和众数都是3 | B. | 中位数为3 | ||
| C. | 方差为10 | D. | 标准差是$\frac{{\sqrt{15}}}{3}$ |
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |