题目内容
7．在平面直角坐标系中，已知点A（1，1），B（3，2），点C在坐标轴上，若△ABC是等腰三角形，则点C的个数是（ ）| A． | 3 | B． | 4 | C． | 7 | D． | 8 |
分析 本题是开放性试题，由题意知A、B是定点，C是动点，所以要分情况讨论：以AC、AB为腰、以AC、BC为腰或以BC、AB为腰．则满足条件的点C可求．
解答 
解：如图，
由题意可知：以AC、AB为腰的三角形有3个；
以AC、BC为腰的三角形有2个；
以BC、AB为腰的三角形有2个．
则点C的个数是7．
故选C．
点评 本题考查了等腰三角形的判定及坐标与图形的性质；分类别寻找是正确解答本题的关键．
练习册系列答案
相关题目
．
18．2015年双十一期间，某网店对一品牌服装进行优惠促销，将原价a元的服装以（$\frac{4}{5}$a-20）元售出，则以下四种说法中可以准确表达该商店促销方法的是（ ）
| A． | 将原价降低20元之后，再打8折 | B． | 将原价打8折之后，再降低20元 | ||
| C． | 将原价降低20元之后，再打2折 | D． | 将原价打2折之后，再降低20元 |
15．若（x+a）（x+b）的积中不含x项，则a，b的关系是（ ）
| A． | 互为倒数 | B． | 互为相反数 | C． | a=b=0 | D． | ab=0 |
如图，L1反映了某公司产品的销售收入与销售量的关系，L2反映了该公司的销售成本与销售量的关系．观察图象．回答下列问题．
12．下列各式不成立的是（ ）
| A． | $-y={（\sqrt{-y}）^2}（y＜0）$ | B． | $-7={（\root{3}{-7}）^3}$ | C． | $-7={（\sqrt{-7}）^2}$ | D． | $-11=-\sqrt{（-11}{）^2}$ |
如图所示，在平行四边形ABCD中，AB=10厘米，AD=12厘米，BC边上的高AE长8厘米，求：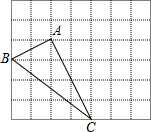
如图，每个小正方形的边长均为1个长度单位的网格中，有一个△ABC，三角形的三个顶点均在网格的顶点上．