题目内容
18. 已知△ABC,作△DEF,使之与△ABC相似,且$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=4.要求:
已知△ABC,作△DEF,使之与△ABC相似,且$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=4.要求:(1)尺规作图,保留作图痕迹,不写作法.
(2)简要叙述作图依据.
分析 (1)利用相似三角形的性质得出:△DEF的边长与△ABC边长的关系进而得出答案;
(2)利用相似三角形的性质结合作三角形的方法得出答案.
解答  解:(1)如图所示:△DEF即为所求;
解:(1)如图所示:△DEF即为所求;
(2)∵△DEF∽△ABC,且$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=4,
∴$\frac{DE}{AB}$=$\frac{DF}{AC}$=$\frac{EF}{BC}$=2,
∴当AB=BE,AC=CF,A点与D点重合,此时△DEF符合题意.
点评 此题主要考查了相似变换以及三角形的做法,正确得出△DEF边长变化规律是解题关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
9.某校的一间礼堂,第1排的座位数为12,从第2排开始,每一排都比前一排增加x个座位.
(1)请在空格里填写适当的代数式.
(2)已知第15排座位数是第5排座位数的2倍,求第25排有多少个座位?
(1)请在空格里填写适当的代数式.
| 第1排 座位数 | 第2排 座位数 | 第3排 座位数 | 第4排 座位数 | 第5排 座位数 | … | 第15排 座位数 | … |
| 12 | 12+x | 12+2x | 12+3x | 12+4x | … | 12+14x | … |
3.一个多边形的内角和是外角和的3倍,则这个多边形的边数( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
10.多项式4ab2+16a2b2-12a3b2c的公因式是( )
| A. | 4ab2c | B. | ab2 | C. | 4ab2 | D. | 4a3b2c |
 如图,5х5方格中,已有5个阴影小正方形,请再选取一个小正方形,使所选的小正方形和阴影部分组合后能折叠成一个正方体.把所有可能的选择都标记出来,直接在图中把所选的小正方形标上序号①②③….
如图,5х5方格中,已有5个阴影小正方形,请再选取一个小正方形,使所选的小正方形和阴影部分组合后能折叠成一个正方体.把所有可能的选择都标记出来,直接在图中把所选的小正方形标上序号①②③….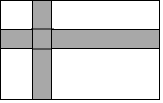 如图,在宽为20m,长为32m的矩形地面上,修筑同样宽的道路(即图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.
如图,在宽为20m,长为32m的矩形地面上,修筑同样宽的道路(即图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.