Question

如图1，在平面直角坐标系中，A（0，n），C（m，0），双曲线y=

12

x

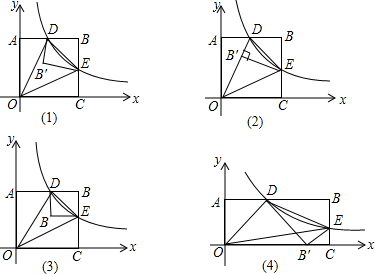
（x＞0）与矩形OABC的两边AB、BC分别交于D、E两点，连接OD、OE、DE，将△DBE沿DE翻折后得△DB′E．
探究一：如图2，若点D为AB中点时，点B′又恰好落在线段OD上，证明：OE平分∠DOC；
探究二：如图3，若OE平分∠DOC，当四边形DB′EB是正方形时，求矩形OABC的面积；
探究三：如图4，若点D在直线y=

4

3

x上，是否存在m的值使B′点落在x轴上，若存在，求出点E的坐标；若不存在，请说明理由．

Answer 1

考点：反比例函数综合题

专题：

分析：探究一：证明OE平分∠DOC可转化为证明BE=B'E，即证明E是BC的中点即可，根据D、E的坐标满足函数的解析式即可证得；
探究二：证明四边形OABC是正方形，易证△AOD≌△COE，即可求得∠COE=

1

3

∠AOC=30°，则OC和CE的比值是

3

：1，则可利用CE的长表示出E的坐标，代入反比例函数解析式，即可求得OC的长，则面积即可求解；
探究三：首先解方程组求得D的坐标，作DF⊥OC于点F，则△ECB'∽△B'FD，利用m表示出EB'的长度，根据相似三角形的对应边的比相等求得B′F的长，即可求得DB'，求得AB的长，则E的横坐标即可求得，代入反比例函数解析式即可求得纵坐标．

解答：探究一：证明：∵A（0，n），C（m，0），
∴B的坐标是（m，n），
∴D的坐标是：（

1

2

m，n），
∵D在线y=

12

x

（x＞0）上，
∴

1

2

mn=12，
又∵E的横坐标是m，把x=m代入y=

12

x

（x＞0），则y=

1

2

n，
∴E是BC的中点，即BE=EC，
又∵B'E=BE，
∴B'E=EC，
∴E在∠DOC的平分线上，即OE平分∠DOC；

探究二：解：设正方形的边长是a，则AD=m-a，CE=n-a，
则D的坐标是：（m-a，n），E的坐标是（m，n-a），
则（m-a）n=m（n-a）=12，
∴m=n．
∴四边形OABC是正方形．
则△AOD≌△COE，
∴∠AOD=∠COE，
又∵∠DOE=∠COE，
∴∠COE=

1

3

∠AOC=30°，
设CE=x，则OC=

3

x，
则E的坐标是（

3

x，x），代入y=

12

x

得：

3

x²=12，
则x²=4

3

，
则正方形OABC的面积是（

3

x）²=3x²=12

3

；

探究三、解：根据题意得：

y= 4 3 x y= 12 x

，
解得：

x=3 y=4

或

x=-3 y=-4

（舍去），
则D的坐标是（3，4）．
C的横坐标是m，则B的横坐标是m，则BD=B'D=a-3，
在y=

12

x

中，当x=m时，y=

12

m

，则CE=

12

m

，BE=B'E=4-

12

m

，
作DF⊥OC于点F．
则△ECB'∽△B'FD，
∴

EC

B′F

=

B′E

B′D

=

4- 12 m

m-3

=

4

m

，
则

12 m

B′F

=

4

m

，
解得：B′F=3，
在直角△DFB'中，DB'=5，
则DB=5，
∴AB=3+5，
∴m=3+8
把x=m=8代入y=

12

x

中得：y=

12

8

=

3

2

．
则E的坐标是（8，

3

2

）．

点评：本题考查了反比例函数的性质以及正方形的性质，相似三角形的判定与性质，正确根据△ECB'∽△B'FD，利用m表示出EB'的长度，根据相似三角形的对应边的比相等求得B′F的长是解本题的关键．