题目内容
阅读下列材料:
x+
=c+
的解是x1=c,x2=
;
x-
=c-
的解是x1=c,x2=-
;
x+
=c+
的解是x1=c,x2=
;
x+
=c+
的解是x1=c,x2=
;
…
(1)请观察上述方程与解的特征,猜想方程x+
=c+
的解,并验证你的结论.
(2)利用这个结论解关于x的方程:x+
=a+
.
x+
| 1 |
| x |
| 1 |
| c |
| 1 |
| c |
x-
| 1 |
| x |
| 1 |
| c |
| 1 |
| c |
x+
| 2 |
| x |
| 2 |
| c |
| 2 |
| c |
x+
| 3 |
| x |
| 3 |
| c |
| 3 |
| c |
…
(1)请观察上述方程与解的特征,猜想方程x+
| m |
| x |
| m |
| c |
(2)利用这个结论解关于x的方程:x+
| 2 |
| x-1 |
| 2 |
| a-1 |
考点:解分式方程
专题:阅读型
分析:根据观察等式,可发现规律,根据规律,可得答案.
解答:解:(1)猜想方程x+
=c+
的解是x1=c,x2=
.
验证:当x=c时,方程x+
=c+
成立,当x=
时,方程x+
=c+
成立;
(2)x+
=a+
变形为(x-1)+
=(a-1)+
,
x-1=a-1或x-1=
∴x=a或x=
.
| m |
| x |
| m |
| c |
| m |
| c |
验证:当x=c时,方程x+
| m |
| x |
| m |
| c |
| m |
| c |
| m |
| x |
| m |
| c |
(2)x+
| 2 |
| x-1 |
| 2 |
| a-1 |
| 2 |
| x-1 |
| 2 |
| a-1 |
x-1=a-1或x-1=
| 2 |
| a-1 |
∴x=a或x=
| a+1 |
| a-1 |
点评:本题考查了解分式方程,观察等式发现规律是解题关键.

练习册系列答案
相关题目
甲、乙两家汽车销售公司根据近几年的销售量分别制作如下统计
从2002~2006年,这两家公司中销售量增长较快的是( )公司.

从2002~2006年,这两家公司中销售量增长较快的是( )公司.
| A、甲公司 | B、乙公司 |
| C、一样快 | D、无法比较 |
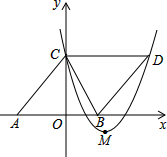 如图,在平面直角坐标系xOy中,菱形ABDC的边AB在x轴上,顶点C在y轴上,A(-6,0),C(0,8),抛物线y=ax2-10ax+c经过点C,且顶点M在直线BC上,则抛物线解析式为
如图,在平面直角坐标系xOy中,菱形ABDC的边AB在x轴上,顶点C在y轴上,A(-6,0),C(0,8),抛物线y=ax2-10ax+c经过点C,且顶点M在直线BC上,则抛物线解析式为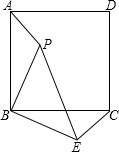 已知:点P是正方形内一点,△ABP旋转后能与△CBE重合.
已知:点P是正方形内一点,△ABP旋转后能与△CBE重合. 如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足
如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足 如图,△ABC为等腰三角形,AB=AC,BD为角平分线,延长BC到E,使CE=CD,作DH⊥BE,垂足为H.
如图,△ABC为等腰三角形,AB=AC,BD为角平分线,延长BC到E,使CE=CD,作DH⊥BE,垂足为H.