题目内容
14.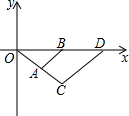 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为( )| A. | (1,-2) | B. | (-2,1) | C. | ($\sqrt{2},-\sqrt{2}$) | D. | (1,-1) |
分析 首先利用等腰直角三角形的性质得出A点坐标,再利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,ky),进而求出即可.
解答 解:∵∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,点B的坐标为(1,0),
∴BO=1,则AO=AB=$\frac{\sqrt{2}}{2}$,
∴A($\frac{1}{2}$,-$\frac{1}{2}$),
∵等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,
∴点C的坐标为:(1,-1).
故选:D.
点评 此题主要考查了位似变换的性质,正确理解位似与相似的关系,记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键.

练习册系列答案
相关题目
2. 如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )
如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )
 如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )
如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )| A. | AC⊥BD | B. | AB=AC | C. | ∠ABC=90° | D. | AC=BD |
19.下列运算正确的是( )
| A. | a+2a=2a2 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | (x-3)2=x2-9 | D. | -2-2=-$\frac{1}{4}$ |
12.下列是二次根式的是( )
| A. | $\root{3}{2}$ | B. | $\sqrt{-2}$ | C. | $\sqrt{(-2)^{2}}$ | D. | $\sqrt{a}$ |
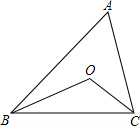 如图,∠ABC=40°,∠ACB=60°,BO、CO平分∠ABC和∠ACB,则∠BOC=130°.
如图,∠ABC=40°,∠ACB=60°,BO、CO平分∠ABC和∠ACB,则∠BOC=130°.