题目内容
4.如图1所示,过点M作⊙N的切线MA、MB,切点分别为A、B,连接MN(1)求证:∠AMN=∠BMN.
(2)如图2所示,在图1的基础上作⊙M,过⊙N的圆心N作⊙M的切线NC、ND,切点分别为C、D,MA、MB分别与⊙M交于点E、F,NC、ND分别与⊙N交于点G、H,MA与ND交于点P.求证:sin∠DPM=$\frac{ME}{MP}$.
(3)求证:四边形EFGH是矩形.
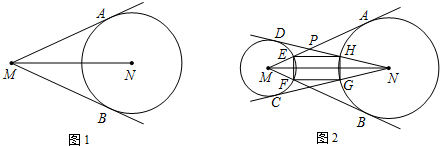
分析 (1)首先连接NA,NB,由MA、MB是⊙N的切线,利用HL易证得Rt△AMN和Rt△BMN,继而证得结论;
(2)首先连接MD,由ND是⊙M的切线,可求得sin∠DPM=$\frac{MD}{MP}$,继而证得sin∠DPM=$\frac{ME}{MP}$;
(3)易证得EH∥MN,继而证得∠FEH=90°,∠EFG=∠FGH=90°,则可证得结论.
解答 证明: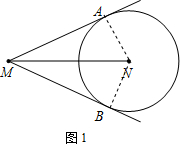 (1)如图,连接NA、NB,
(1)如图,连接NA、NB,
∵MA、MB是⊙N的切线,
∴∠MAN=∠MBN=90°,
在Rt△AMN和Rt△BMN中,
$\left\{\begin{array}{l}{NA=NB}\\{MN=MN}\end{array}\right.$,
∴Rt△AMN和Rt△BMN(HL),
∴∠AMN=∠BMN;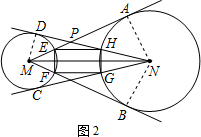 (2)如图2,连接MD,
(2)如图2,连接MD,
∵ND是⊙M的切线,
∴∠MDP=90°,
∴sin∠DPM=$\frac{MD}{MP}$,
∵MD=ME,
∴sin∠DPM=$\frac{ME}{MP}$;
(3)由(2)可得sin∠APN=$\frac{NH}{NP}$,
∴$\frac{ME}{MP}$=$\frac{NH}{NP}$,
∴EH∥MN,
∵ME=MF,∠AMN=∠BMN,
∴MN⊥EF,
∴EH⊥EF,
∴∠FEH=90°,
同理可证∠EFG=∠FGH=90°,
∴四边形EFGH是矩形.
点评 此题属于圆的综合题,考查了切线的性质、全等三角形的判定与性质、矩形的判定以及三角函数等知识.注意准确作出辅助线是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
 已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )| A. | 外心 | B. | 内心 | C. | 重心 | D. | 无法确定 |
15.若a>b,且c为实数,有下列各式:
①ac>bc;②ac<bc;③ac2>bc2;④ac2≥bc2;⑤$\frac{a}{c}$>$\frac{b}{c}$
其中,正确的有( )
①ac>bc;②ac<bc;③ac2>bc2;④ac2≥bc2;⑤$\frac{a}{c}$>$\frac{b}{c}$
其中,正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16. 如图所示的三棱柱的正视图是( )
如图所示的三棱柱的正视图是( )
 如图所示的三棱柱的正视图是( )
如图所示的三棱柱的正视图是( )| A. |  | B. |  | C. |  | D. |  |
14.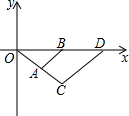 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为( )
 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为( )| A. | (1,-2) | B. | (-2,1) | C. | ($\sqrt{2},-\sqrt{2}$) | D. | (1,-1) |
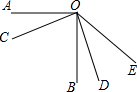 如图,已知∠AOB=∠COD=90°,∠AOC=20°45′,∠DOE=26°58′,则∠BOE=47°43′.
如图,已知∠AOB=∠COD=90°,∠AOC=20°45′,∠DOE=26°58′,则∠BOE=47°43′.