题目内容
9.从1到10的十个自然数中,随意取出一个数,该数为3的倍数的概率是$\frac{3}{10}$.分析 由从1到10的十个自然数中,是3的倍数的有3,6,9,直接利用概率公式求解即可求得答案.
解答 解:∵从1到10的十个自然数中,是3的倍数的有3,6,9,
∴随意取出一个数,该数为3的倍数的概率是:$\frac{3}{10}$.
故答案为:$\frac{3}{10}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
20. 如图,菱形ABCD中,点O对角线AC的三等分点,连接OB、OD,且OB=OC=OD.已知AC=3,那么菱形的边长为( )
如图,菱形ABCD中,点O对角线AC的三等分点,连接OB、OD,且OB=OC=OD.已知AC=3,那么菱形的边长为( )
 如图,菱形ABCD中,点O对角线AC的三等分点,连接OB、OD,且OB=OC=OD.已知AC=3,那么菱形的边长为( )
如图,菱形ABCD中,点O对角线AC的三等分点,连接OB、OD,且OB=OC=OD.已知AC=3,那么菱形的边长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
14.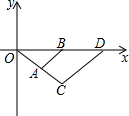 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为( )
 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为( )| A. | (1,-2) | B. | (-2,1) | C. | ($\sqrt{2},-\sqrt{2}$) | D. | (1,-1) |
1.|-4|等于( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
6.下列计算正确的是( )
| A. | 2a-a=2 | B. | m6÷m2=m3 | ||
| C. | x2010+x2010=2x2010 | D. | t2-t3=t6 |
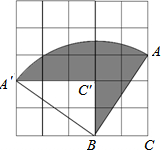 如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B逆时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则图中阴影部分的面积约是$\frac{13π}{4}$π-3.(保留π)
如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B逆时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则图中阴影部分的面积约是$\frac{13π}{4}$π-3.(保留π)