题目内容
11．先化简再求值：a+{b-2a+[3a-2（b+2a）+5b]}，其中a，b满足2（a-$\frac{1}{2}$）2+|b+1|=0．分析 首先去括号进而合并同类项，再利用已知求出a，b的值，进而求出答案．
解答 解：a+{b-2a+[3a-2（b+2a）+5b]}
=a+[b-2a+3a-2（b+2a）+5b]
=a+（6b+a-2b-4a）
=a+4b-3a
=4b-2a，
∵2（a-$\frac{1}{2}$）2+|b+1|=0，
∴a=$\frac{1}{2}$，b=-1，
则原式=4×（-1）-2×$\frac{1}{2}$
=-5．
点评 此题主要考查了整式的化简求值，正确得出a，b的值是解题关键．
练习册系列答案
相关题目
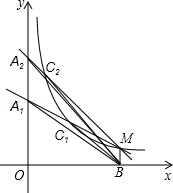如图，点M是反比例函数y=$\frac{2}{x}$在第一象限内图象上的点，作MB⊥x轴于B．过点M的第一条直线交y轴于点A1，交反比例函数图象于点C1，且A1C1=$\frac{1}{2}$A1M，△A1C1B的面积记为S1；过点M的第二条直线交y轴于点A2，交反比例函数图象于点C2，且A2C2=$\frac{1}{4}$A2M，△A2C2B的面积记为S2；过点M的第三条直线交y轴于点A3，交反比例函数图象于点C3，且A3C3=$\frac{1}{8}$A3M，△A3C3B的面积记为S3；以此类推…；S1+S2+S3+…+S6=$\frac{63}{64}$．
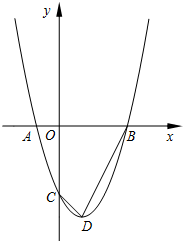如图，O是坐标原点，过点A（-1，0）的抛物线y=x2-bx-3与x轴的另一个交点为B，与y轴交于点C，其顶点为D点．
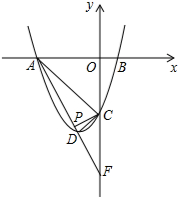如图，已知抛物线y=ax2+bx+c与x轴交于点A、B（2，0），与直线AC：y=-x-6交y轴于点C，点D是抛物线的顶点．