��Ŀ����
20��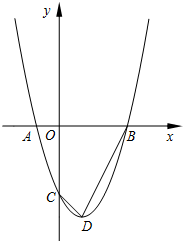 ��ͼ��O������ԭ�㣬����A��-1��0����������y=x2-bx-3��x�����һ������ΪB����y�ύ�ڵ�C���䶥��ΪD�㣮
��ͼ��O������ԭ�㣬����A��-1��0����������y=x2-bx-3��x�����һ������ΪB����y�ύ�ڵ�C���䶥��ΪD�㣮��1����b��ֵ�Լ�D�����꣮
��2����x�����Ƿ���ڵ�P����ʹ�á�ACP���BCD���ƣ������ڣ������P�����꣬�������ڣ�˵�����ɣ�
��3������BD��CD������Q��������m��1����
�ٵ��ı���BQCD��ƽ���ı���ʱ����m��ֵ��
������OQ��CQ�����CQO�����Բ�뾶����Сֵ���������Q�����꣮
���� ��1�����ݴ���ϵ�������ɵú�������ʽ�������䷽�����ɵö������ꣻ
��2���������������ε����ʣ��ɵ�AP�ij��������߶εĺͲ�ɵ�P�����ꣻ
��3���ٸ����Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�B��C��D�Ĺ�ϵ�������߶εĺͲ�ɵ�FC�ij�������ƽ���ı��ε����ʣ��ɵ�CQ�ij������ݹ��ɶ������ɵ�FQ�ij���
�ڸ��������ε������ڱߵĴ�ֱƽ�����ϣ��ɵ�M��OC�Ĵ�ֱƽ�����ϣ��������ߵ�����MQ=FN�����ݹ��ɶ������ɵ�MN�ij����ɵô𰸣�
��� �⣺��1����A��-1��0������y=x2-bx-3����
1+b-3=0��
���b=2��
y=x2-2x-3=��x-1��2-4����D��1��-4����
��2����ͼ1 ��
��
��y=0ʱ��x2-2x-3=0�����x1=-1��x2=3����A��-1��0����B��3��0����D��1��-4����
�ɹ��ɶ�������
BC2=18��CD2=1+1=2��BD2=22+16=20��
BC2+CD2=BD2����BCD=90�㣬
�ٵ���APC��DCBʱ��$\frac{AP}{CD}$=$\frac{CP}{BC}$����$\frac{AP}{\sqrt{2}}$=$\frac{3}{3\sqrt{2}}$�����AP=1����P��0��0����
�ڵ���ACP�ס�DCBʱ��$\frac{AP}{BD}$=$\frac{AC}{CD}$����$\frac{AP}{2\sqrt{5}}$=$\frac{\sqrt{10}}{\sqrt{2}}$�����AP=10����P�䣨9��0����
������������P�����꣨0��0����9��0����
��3������ͼ2 ��
��
�������ߵĶԳ�����x�ύ��E�㣬��OE=1��DE=4��
��x=0ʱ��y=-3����C��0��-3����
��y=0ʱ��x2-2x-3=0��
���x1=-1��x2=3��
OB=3��OC=3��BE=2��
��ֱ��y=1��y�ύ�ڵ�F��
CF=4��BD=$\sqrt{D{E}^{2}+B{E}^{2}}$=2$\sqrt{5}$��
���ı���BQCD��ƽ���ı���ʱ��CQ=BD=2$\sqrt{5}$��
��CF=OF+OC=1+3=4��
��FQ=$\sqrt{C{Q}^{2}-C{F}^{2}}$=2��
m=FQ=2��
����ͼ3 ��
��
�ǡ�OQC������ΪM����M��OC�Ĵ�ֱƽ����MN�ϣ�MN��y�ύ���N����
�ߵ�MQȡ��Сֵʱ��
��M��ֱ��y=1���У�
MQ=FN=OM=2.5��
MN=$\sqrt{O{M}^{2}-O{N}^{2}}$=$\sqrt{2��{5}^{2}-1��{5}^{2}}$=2��
FQ=MN=2��
��Q��2��1����
���� ���⿼���˶��κ����ۺ��⣬�����䷽�������Ķ������ꣻ��2���������������ε����ʵó�����AP�ķ����ǽ���ؼ���Ҫ�������ۣ��Է���©����3�����ù��ɶ����ó�����FQ��ֵ�ǽ���ؼ���

| A�� | 10 | B�� | 8 | C�� | 6��10 | D�� | 8��10 |
 ��ͼ��A��B����ת�̷ֱ�ƽ���ֳ��������ĸ����Σ��ֱ�ת��A�̡�B�̸�һ�Σ�ת�������У�ָ�뱣�ֲ��������ָ��ǡ��ָ�ڷָ����ϣ�����תһ�Σ�ֱ��ָ��ָ��һ���������ڵ�����Ϊֹ������ת��ֹͣ��ָ����ָ�����ڵ�����֮��С��6�ĸ�����$\frac{1}{2}$��
��ͼ��A��B����ת�̷ֱ�ƽ���ֳ��������ĸ����Σ��ֱ�ת��A�̡�B�̸�һ�Σ�ת�������У�ָ�뱣�ֲ��������ָ��ǡ��ָ�ڷָ����ϣ�����תһ�Σ�ֱ��ָ��ָ��һ���������ڵ�����Ϊֹ������ת��ֹͣ��ָ����ָ�����ڵ�����֮��С��6�ĸ�����$\frac{1}{2}$��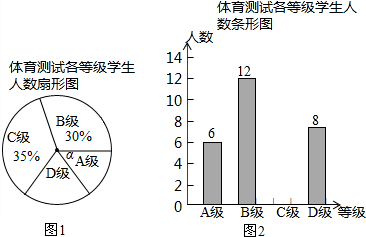
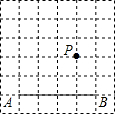 ��ͼ���ڷ���ֽ�У���A��B��P���ڸ���ϣ��밴Ҫ����ABΪ�ߵĸ���ı��Σ�ʹP���ı����ڲ����������߽��ϣ�����P���ı��ε���������ľ�����ȣ�
��ͼ���ڷ���ֽ�У���A��B��P���ڸ���ϣ��밴Ҫ����ABΪ�ߵĸ���ı��Σ�ʹP���ı����ڲ����������߽��ϣ�����P���ı��ε���������ľ�����ȣ� ��֪AB�ǰ뾶Ϊ1��ԲOֱ����C��Բ��һ�㣬D��BC�ӳ�����һ�㣬����D��ֱ�߽�AC��E�㣬�ҡ�AEFΪ�ȱ�������
��֪AB�ǰ뾶Ϊ1��ԲOֱ����C��Բ��һ�㣬D��BC�ӳ�����һ�㣬����D��ֱ�߽�AC��E�㣬�ҡ�AEFΪ�ȱ������� ������ڼ䣬ij�̳�Ϊ�������˿ͣ�������һ����������ת����ת�̣�ת�̱�ƽ���ֳ�16�ݣ������涨���˿�ÿ����100Ԫ����Ʒ�����ܻ��һ��תת�̵Ļ��ᣬ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ���˿;Ϳ��Էֱ�������ܡ�ͯ���顢ˮ�ʱʣ�С�������蹺����125Ԫ����Ʒ������������㣺
������ڼ䣬ij�̳�Ϊ�������˿ͣ�������һ����������ת����ת�̣�ת�̱�ƽ���ֳ�16�ݣ������涨���˿�ÿ����100Ԫ����Ʒ�����ܻ��һ��תת�̵Ļ��ᣬ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ���˿;Ϳ��Էֱ�������ܡ�ͯ���顢ˮ�ʱʣ�С�������蹺����125Ԫ����Ʒ������������㣺