题目内容
16．不等式组$\left\{\begin{array}{l}{2}\;x+1＞0\\ x＞2x-5\end{array}\right.$的正整数解为1，2，3，4．分析 首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集，然后确定解集中的正整数解即可．
解答 解：$\left\{\begin{array}{l}{2x+1＞0…①}\\{x＞2x-5…②}\end{array}\right.$，
解①得：x＞-$\frac{1}{2}$，
解②得x＜5，
则不等式的解集是-$\frac{1}{2}$＜x＜5．
则正整数解是：1，2，3，4．
故答案是：1，2，3，4．
点评 此题考查的是一元一次不等式组的解法，求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
相关题目
6．若反比例函数的图象经过点（-1，2），则这个图象必经过点（ ）
| A． | （1，2） | B． | （-1，-2） | C． | （2，-1） | D． | （2，1） |
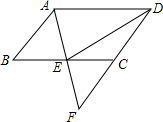如图，在?ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．
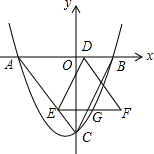如图，抛物线y=ax2+bx-4经过A（-3，0）、B（2，0）两点，与y轴的交点为C，连接AC、BC，D为线段AB上的动点，DE∥BC交AC于E，A关于DE的对称点为F，连接DF、EF．
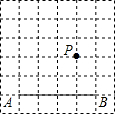如图，在方格纸中，点A，B，P都在格点上．请按要求画出以AB为边的格点四边形，使P在四边形内部（不包括边界上），且P到四边形的两个顶点的距离相等．