题目内容
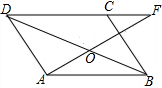已知，如图，平行四边形ABCD中，F点是DC延长线上的一点，AF交BD于O，交BC于E．求证：（1）OA2=OE•OF；
（2）BE：AB=BC：DF．
考点：相似三角形的判定与性质,平行四边形的性质
专题：证明题
分析：（1）证明△AOD∽△EOB，△DOF∽△BOA，得到
=
，
=
，即可解决问题．
（2）证明
=
；证明BC=AD，即可解决问题．
| OF |
| OA |
| OD |
| OB |
| OA |
| OE |
| OD |
| OB |
（2）证明
| BE |
| AB |
| AD |
| DF |
解答：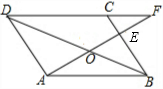
证明：（1）∵四边形ABCD为平行四边形，
∴AB∥DF、AD∥BC，
∴△AOD∽△EOB，△DOF∽△BOA，
∴
=
，
=
，
∴
=
，
即OA2=OE•OF．
（2）∵△AOD∽△EOB，△DOF∽△BOA，
∴
=
，
=
，
∴
=
，
∴
=
；
∵四边形ABCD为平行四边形，
∴BC=AD，
∴BE：AB=BC：DF．
证明：（1）∵四边形ABCD为平行四边形，∴AB∥DF、AD∥BC，
∴△AOD∽△EOB，△DOF∽△BOA，
∴
| OF |
| OA |
| OD |
| OB |
| OA |
| OE |
| OD |
| OB |
∴
| OF |
| OA |
| OA |
| OE |
即OA2=OE•OF．
（2）∵△AOD∽△EOB，△DOF∽△BOA，
∴
| AD |
| BE |
| DO |
| OB |
| DF |
| AB |
| DO |
| OB |
∴
| AD |
| BE |
| DF |
| AB |
∴
| BE |
| AB |
| AD |
| DF |
∵四边形ABCD为平行四边形，
∴BC=AD，
∴BE：AB=BC：DF．
点评：该题以平行四边形为载体，以考查相似三角形的判定及其性质的应用为核心构造而成；对综合的分析问题解决问题的能力提出了一定的要求．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
如图，在长为32m，宽为20m的矩形耕地上，修筑同样宽的三条道路，使得剩余面积作为实验田，要使试验田面积为570m2，道路的宽应为多少？
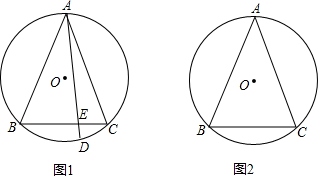
已知：如图，四边形ABCD内接于圆，DP∥CA交BA延长线于P．求证：AD•DC=PA•CB．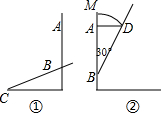
如图①，AB是房间的一面窗户的高，A是窗户上端，B是窗户下端，太阳光按BC的方向射入房间．