题目内容
5．学校团委在“五四青年节”举行“感动校园十大人物”颁奖活动中，九（4）班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动，则甲乙丙三人恰有两人参加此活动的概率是$\frac{1}{2}$．分析 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与甲乙丙三人恰有两人参加此活动的情况，再利用概率公式即可求得答案．
解答 解：画树状图得：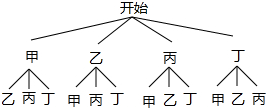
∵共有12种等可能的结果，甲乙丙三人恰有两人参加此活动的有6种情况，
∴甲乙丙三人恰有两人参加此活动的概率是：$\frac{6}{12}$=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
阅读快车系列答案
相关题目
15．我校举行了“建设宜居中山，关注环境保护”的知识竞赛，某班学生的成绩统计如下：
则该班学生成绩的众数和中位数分别是（ ）
| 成绩（分） | 60 | 70 | 80 | 90 | 100 |
| 人数 | 4 | 8 | 12 | 11 | 5 |
| A． | 70分，80分 | B． | 80分，80分 | C． | 90分，80分 | D． | 80分，90分 |
16．某公司根据市场计划调整投资策略，对A，B两种产品进行市场调查，收集数据如表：
其中m是待定常数，其值是由生产A的材料的市场价格决定的，变化范围是6≤m≤8，销售B产品时需缴纳$\frac{1}{20}$x2万元的关税，其中x为生产产品的件数，假定所有产品都能在当年售出，设生产A，B两种产品的年利润分别为y1、y2（万元），写出y1、y2与x之间的函数关系式，注明其自变量x的取值范围．
| 项目 产品 | 年固定成本 （单位：万元） | 每件成本 （单位：万元） | 每件产品销售价 （万元） | 每年最多可生产的件数 |
| A | 20 | m | 10 | 200 |
| B | 40 | 8 | 18 | 120 |
13．在一次知识竞赛中，学校为获得一等奖和二等奖共30名学生购买奖品，共花费528元，其中一等奖奖品每件20元，二等奖奖品每件16元，求获得一等奖和二等奖的学生各有多少名？设获得一等奖的学生有x名，二等奖的学生有y名，根据题意可列方程组为（ ）
| A． | $\left\{\begin{array}{l}{x+y=528}\\{20x+16y=30}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=30}\\{20x+16y=528}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=30}\\{\frac{x}{30}+\frac{y}{16}=528}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=528}\\{\frac{x}{20}+\frac{y}{16}=30}\end{array}\right.$ |
20．甲、乙两人进行射击测试，每人10次射击成绩的平均数都是8.5环，方差分别是：S${\;}_{甲}^{2}$=2，S${\;}_{乙}^{2}$=1.5，根据以上数据，下列说法正确的是（ ）
| A． | 甲的成绩比乙的成绩稳定 | B． | 乙的成绩比甲的成绩稳定 | ||
| C． | 甲、乙两人的成绩一样稳定 | D． | 无法确定甲、乙的成绩谁更稳定 |
10．下列命题错误的是（ ）
| A． | 已知菱形的两条对角线长分别是a、b，则这个菱形的面积为$\frac{1}{2}$ab | |
| B． | 在Rt△ABC中，若∠C=90°，∠A=30°，则AB=2CD | |
| C． | 在平面直角坐标系中，到x轴的距离为2，到y轴的距离为3的点的坐标是（3，2） | |
| D． | 在平面直角坐标系中，已知点P（2，-2），将线段OP绕着点O按顺时针方向旋转90°到OP′，则点P′的坐标是（-2，-2） |
如图，点B、C、E在同一条直线上，请你写出一个能使AB∥CD成立的条件：∠1=∠2．（只写一个即可，不添加任何字母或数字）
16．
如图，△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为（ ）
如图，△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为（ ）| A． | 30° | B． | 36° | C． | 45° | D． | 70° |