题目内容
13.在一次知识竞赛中,学校为获得一等奖和二等奖共30名学生购买奖品,共花费528元,其中一等奖奖品每件20元,二等奖奖品每件16元,求获得一等奖和二等奖的学生各有多少名?设获得一等奖的学生有x名,二等奖的学生有y名,根据题意可列方程组为( )| A. | $\left\{\begin{array}{l}{x+y=528}\\{20x+16y=30}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=30}\\{20x+16y=528}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=30}\\{\frac{x}{30}+\frac{y}{16}=528}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=528}\\{\frac{x}{20}+\frac{y}{16}=30}\end{array}\right.$ |
分析 由获得一等奖的学生有x名,二等奖的学生有y名,根据“一等奖和二等奖共30名学生”,“一等奖和二等奖共花费528元,”列出方程组.
解答 解:由题意得:$\left\{\begin{array}{l}{x+y=30}\\{20x+16y=528}\end{array}\right.$.
故选B.
点评 此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系,列出方程组.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.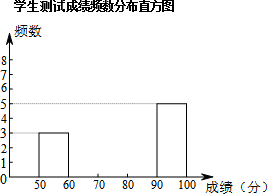 某校九年级有200名学生参加《中小学生国家体质健康标准》测试赛活动.为了解本次测试的成绩分布情况,从中抽取了20名学生的成绩进行分组整理.现已完成前15个数据的整理,还有后5个数据尚未累计:
某校九年级有200名学生参加《中小学生国家体质健康标准》测试赛活动.为了解本次测试的成绩分布情况,从中抽取了20名学生的成绩进行分组整理.现已完成前15个数据的整理,还有后5个数据尚未累计:
62,83,76,87,70,
学生测试成绩频数分布表
(1)请将剩余的5个数据累计在“学生测试成绩频数分布表”中,填上各组的频数与频率,并补全“学生测试成绩频数分布直方图”;
(2)这20个数据的中位数所在组的成绩范围是80≤x<90;
(3)请估计这次该校九年级参加测试赛的学生中约有多少学生成绩不低于80分.
 某校九年级有200名学生参加《中小学生国家体质健康标准》测试赛活动.为了解本次测试的成绩分布情况,从中抽取了20名学生的成绩进行分组整理.现已完成前15个数据的整理,还有后5个数据尚未累计:
某校九年级有200名学生参加《中小学生国家体质健康标准》测试赛活动.为了解本次测试的成绩分布情况,从中抽取了20名学生的成绩进行分组整理.现已完成前15个数据的整理,还有后5个数据尚未累计:62,83,76,87,70,
学生测试成绩频数分布表
| 成绩x(分) | 频数累计 | 频数 | 频率 |
| 50≤x<60 | 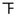 | 3 | 0.15 |
| 60≤x<70 | ▁ | 2 | 0.10 |
| 70≤x<80 | 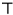 | 4 | 0.20 |
| 80≤x<90 | 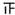 | 6 | 0.30 |
| 90≤x≤100 | 正 | 5 | 0.25 |
| 合计 | 20 | 1.00 |
(2)这20个数据的中位数所在组的成绩范围是80≤x<90;
(3)请估计这次该校九年级参加测试赛的学生中约有多少学生成绩不低于80分.
4.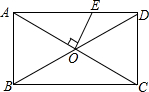 如图所示,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
如图所示,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
 如图所示,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
如图所示,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 1.5 |
8.下列图形中,是中心对称图形而不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为8.
如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为8. 如图,AB与CD相交于点O,且AC∥BD.求证:OA•OD=OC•OB.
如图,AB与CD相交于点O,且AC∥BD.求证:OA•OD=OC•OB.